Часть 1
Задание 1
S
A0 = 1м
2
A0 = 2 × A1 (разрез || меньшей стороне)
A1 = 2 × A2
A2 = 2 × A3
и т.д.
Решение:
По таблице от самых маленьких размеров до самых больших:
A6 — 105 × 148 ⇒ 3
A5 — 148 × 210 ⇒ 4
A4 — 210 × 297 ⇒ 1
A3 — 297 × 420 ⇒ 2
Ответ: 3412
Задание 2
Решение:
По рисунку A0 = 2A1 = 2 × 2 × A2 = 2 × 2 × 2A3 = 2 × 2 × 2 × 2A4 = 2 × 2 × 2 × 2 × 2A5 = 2 × 2 × 2 × 2 × 2 × 2A6 = 2
6 = 64 листа
Ответ: 64
Задание 3
Решение:
1) По рисунку меньшая сторона A2 = большей стороне A3
2) По таблице A3 под номером 2
420 мм — большая сторона
Ответ: 420
Задание 4
S
A5 — ?см
2
Решение:
Размеры A5 — 148мм × 210мм
S = 31080мм
2 = 310.8см
2
Ответ: 310.8
Задание 5
Решение:
h
1 пункта =
172 дюйма = 0.3528мм
По таблице длина A3 = 420мм, длина A4 = 297мм
1)
420297 = 1.4141… = 1.(41) во столько раз больше на A3 чем на A4
2) 1.41 × 10 пунктов = 14.1 пункт ≈ 14 пунктов
Ответ: 14
Задание 6
Решение:
3.52 — 49 = 3.5199 — 49 =
3.5159 = 3
12 : 1
59 =
72 :
149 =
72 ×
914 =
7 × 92 × 14 =
92 × 2 =
94 = 2
14 = 2.25
Ответ: 2.25
Задание 7
Решение:
По рисунку 7 < a < 8
a ≈ 7.7
1) 8 — a > 0 ⇒ a < 8 верно ⇒ 1
2) 8 — a < 0 ⇒ a > 8 неверно
3) a — 7 < 0 ⇒ a < 7 неверно
4) a — 9 > 0 ⇒ a > 9 неверно
Ответ: 1
Задание 8
Решение:
√
a⁶ × (-a)² = √
a⁶ × a² = √
a⁶ ⁺ ² = √
a⁸ = √
(a⁴)² = |a
4| = |3
4| = |81| = 81
Ответ: 81
Задание 9
Решение:
5x
2 + 9x + 4 = 0
a = 5, b = 9, с = 4
D = b
2 — 4ac = 9
2 — 4 × 5 × 4 = 81 — 80 = 1
x
1,2 =
-b ± √D2a =
-9 ± 110
x
1 =
-9 — 110 = —
1010 = -1
x
2 =
-9 + 110 =
-810 = -0.8 больший корень
Ответ: -0.8
Задание 10
Решение:
P
желтых машин = ?
Найдем вероятность подачи желтой машины как отношение количества желтых машин к общему числу машин ⇒
320 = 0.15
Ответ: 0.15
Задание 11
Решение:
y = ax
2 + bx + c — парабола
Если a > 0, то ветви ↑
a < 0, то ветви ↓
Если c > 0, то при x = 0, y > 0
c < 0, то при x = 0, y < 0
А) a > 0, с > 0 ➔ 3
Б) a > 0, c < 0 ➔ 2
В) a < 0, c > 0 ➔ 1
Ответ: 321
Задание 12
Решение:
P = I
2R
R — ?
P = 245, I = 7
245 = 7
2 × R ⇒ R =
24549 = 5
Ответ: 5
Задание 13
Решение:
6x — 3(4x + 1) > 6
6x — 12x — 3 > 6
6x — 12x > 6 + 3
-6x > 9 (разделим обе части неравенства на -6)
x < —
96
x < —
32
x < -1.5
(-∞; -1.5) ➔ 2
Ответ: 2
Задание 14
Решение:
Масса изотопа уменьшается в 2 раза каждые 9 минут.
| Время |
масса изотопа |
| t0 |
320 мг |
| t1 = 9 мин |
320 : 2 = 160 мг |
| t2 = 9 мин |
160 : 2 = 80 мг |
| t3 = 9 мин |
80 : 2 = 40 мг |
| t4 = 9 мин |
40 : 2 = 20 мг |
| t5 = 9 мин |
20 : 2 = 10 мг |
| t6 = 9 мин |
10 : 2 = 5 мг |
| t7 = 9 мин |
5 : 2 = 2.5 мг |
63 мин = 7 × 9 мин
Ответ: 2.5
Задание 15
Решение:
1) Δ ABC — равносторонний
BD — биссектриса ⇒ BD — высота h
2) Используя формулу h =
a√32, где a — сторона треугольника.
Найдем биссектрису BD
BD =
14√3 × √32 =
14 × (√3)22 = 7 × 3 = 21
Ответ: 21
Задание 16
Решение:
ABCD описан около окружности ⇒ AB + CD = BC + AD
11 + 12 = 13 + AD
23 = 13 + AD
AD = 23 — 13 = 10
Ответ: 10
Задание 17
Решение:
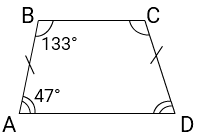
1) ∠ A + ∠ D = 94°
∠ A = ∠ D = 94° : 2 = 47 (по свойству равнобедренной трапеции)
2) ∠ B = 180° — 47° = 133° (т.к. ∠ A и ∠ B — односторонние при AD || BC и секущей AB)
Ответ: 133
Задание 18
Решение:
ABCD — параллелограмм
S
ABCD = AB × CH, где AB — сторона равная 5 клеткам
CH — высота равная 4 клеткам
S
ABCD = 5 × 4 = 20
Ответ: 20
Задание 19
Решение:
1)
AC ≠ BD диагонали ⇒ утверждение неверно.
2)
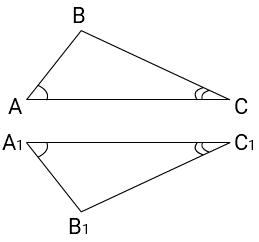
∠ A = ∠ A
1 и ∠ C = ∠ C
1 ⇒ Δ ABC подобен Δ A
1B
1C
1
Утверждение верно.
3)
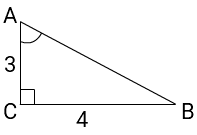
tg A =
BCAC =
43 = 1
13 > 1 ⇒ утверждение неверно.
Ответ: 2
Часть 2
Задание 20
Решение:
x
3 + 4x
2 = 9x + 36
x
3 + 4x
2 — 9x — 36 = 0
x
2(x + 4) — 9(x + 4) = 0
(x + 4)(x
2 — 9) = 0
(x + 4)(x
2 — 3
2) = 0
(x + 4)(x — 3)(x + 3) = 0
x + 4 = 0
x = -4
или
x — 3 = 0
x = 3
или
x + 3 = 0
x = -3
Ответ: -3; 3; -4
Задание 21
Решение:
|
Vкм/ч |
tч |
Sкм |
| I |
x? |
420x |
420 |
| II |
x — 24 |
420x — 24 |
420 |
t
1 < t
2 на 2 часа
t
2 — t
1 = 2
420x — 24 —
420x = 2 умножим обе части уравнения на x(x — 24)
420x — 420x + 420 × 24 = 2x
2 — 48x
2x
2 — 48x — 420 × 24 = 0 разделим обе части уравнения на 2
x
2 — 24x — 420 × 12 = 0
D4 = (
b2)
2 — ac = (-
242)
2 — 1 × (-420 × 12)
D4 = 12
2 + 420 × 12 = 12 × (12 + 420)
D4 = 12 × 432 = 5184 = 72
2
x
1,2 =
— b2 ± √D4a =
-(-12) ± 721
x
1,2 = 12 ± 72
x
1 = 12 + 72 = 84
x
2 = 12 — 72 = -60 < 0
Ответ: 84 км/ч
Задание 22
Решение:
y =
(0.25x2 + x) × |x|x + 4, x ≠ -4
1) Если x ≥ 0, то y =
(14x2 + x)xx + 4
y =
x2(14x + 1)x + 4 =
0.25x2(x + 4)x + 4
y =
14x
2 парабола, ветви ↑
2) Если x < 0, то y =
(14x2 + x) × (-x)x + 4
y =
-0.25x2 × (x + 4)x + 4 = —
14x
2, ветви ↓
3) Построим график y = f(x)
y=
14x
2, x ≥ 0
y = —
14x
2, x < 0, x ≠ -4
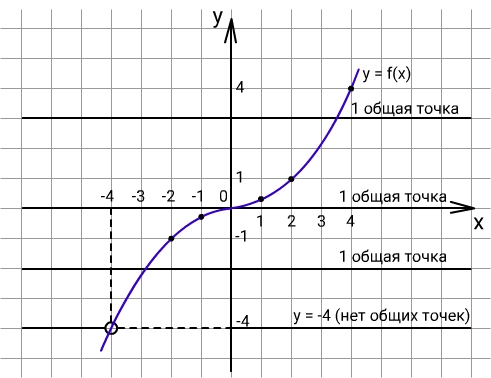
4) Прямая y = m не имеет с y = f(x) ни одной общей точки при m = -4
Ответ: -4
Задание 23
R
окружности описанной около ΔABC = 14
Решение:
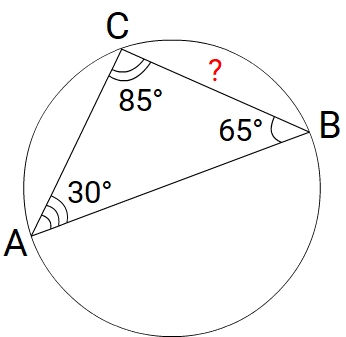
1) ∠ A = 180° — 85° — 65° = 30° (по теореме о сумму углов треугольника)
2)
BCsinA = 2R (следствие из теоремы синусов)
BCsin30° = 2 × 14
BC12 = 2 × 14 ⇒ BC = 2 × 14 ×
12
BC = 14
Ответ: 14
Задание 24
Решение:
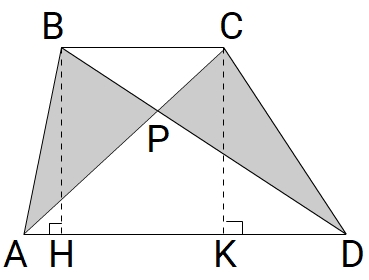
1) Δ ABD и Δ ACD имеют равные высоты BH и CK ⇒ S
ABD = S
ACD
2) S
APD = S
ABD — S
ABP и S
APD = S
AСD — S
PСD ⇒ S
ABD — S
ABP = S
ACD — S
PCD
3) S
ABP = S
PCD что и требовалось доказать.
Ответ: доказано SABP = SPCD
Задание 25
Решение:
1) BE ∩ AD = P
Рассмотрим треугольник ABD — равнобедренный т.к. BP — биссектриса и высота ⇒ BD = BA и BP — медиана т.е. AP = PD = 24 : 2 = 12
2) BC = 2BD т.к. BD = AB, то BC = 2AB
3) BE — биссектриса Δ ABC ⇒
AEAB =
ECCB или
AEEC =
ABCB
ABCB =
AB2AB =
12 ⇒
AEEC =
12 т.к. AC = AE + EC, то AC = 3AE
4) Дополнительное построение BK || AC, BK ∩ AD = K
BK = AC = 3AE
5) Δ APE ⁓ Δ KPB (по двум углам)
∠ BPK = ∠ APE = 90°
∠ A = ∠ K (накрест лежащие углы) ⇒
PEBP =
AEBK =
13 ⇒ BP = 3PE.
Но BE = 24 (по условию)
BE = BP + PE = 24
3PE + PE = 24
4PE = 24
PE = 24 : 4 = 6, тогда BP = 3 × 6 = 18
6) Δ ABP (∠ P = 90°) по теореме Пифагора AB = √
AP² + BP² = √
12² + 18²
AB = √
144 + 324 = √
468 = √
2² × 3² × 13
AB = 2 × 3√13 = 6√13
7) Δ APE (∠ P = 90°) по теореме Пифагора AE = √
AP² + PE² = √
12² + 6²
AE = √
144 + 36 = √
180
AE = √
2² × 3² × 5 = 2 × 3√5 = 6√5
8 ) BC = 2AB = 2 × 6√13 = 12√13
9) AC = 3AE = 3 × 6√5 = 18√5
Ответ: 6√13, 12√13, 18√5
