Решение заданий на вектора ЕГЭ по математике профильный уровень

Вариант 1. Задание 2

(из сборника ЕГЭ 2024 математика профиль Ященко И.В. 50 вариантов) На координатной плоскости изображены векторы a^➔ и b^➔ с целочисленными координатами. Найдите скалярное произведение a^➔ × b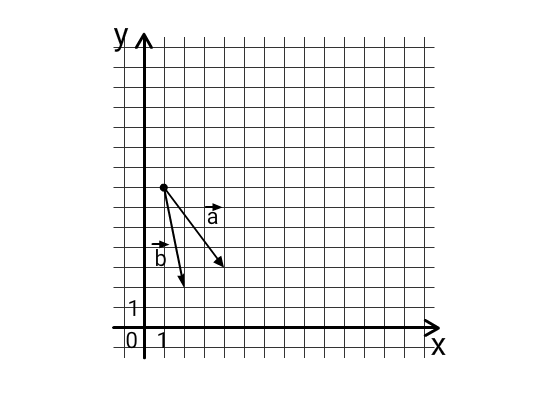^➔. Решение: По рисунку: 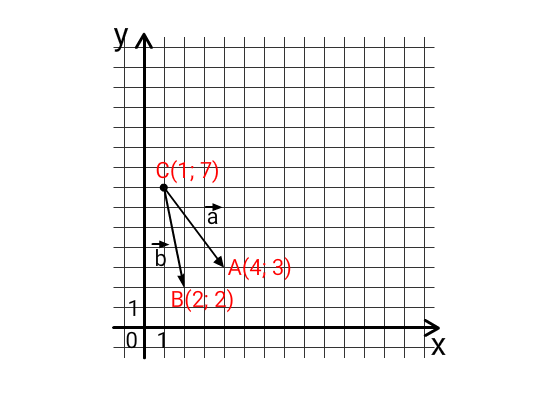1) Пусть a^➔ = CA^➔, где C(1; 7) — начало вектора, A(4; 3) — конец вектора b^➔ = CB^➔, где C(1; 7) — начало вектора, B(2; 2) — конец вектора 2) Найдем координаты вектора CA^➔{4-1; 3-7} = {3; -4} Найдем координаты вектора CB^➔{2-1; 2-7} = {1; -5} (от координат конца вектора отняли координаты его начала). 3) Найдем скалярное произведение векторов по формуле a^➔ × b^➔ = x₁ × x₂ + y₁ × y₂ где a^➔{x₁; y₁} и b^➔{x₂; y₂} тогда a^➔ × b^➔ = CA^➔ × CB^➔ = 3 × 1 + 4 × 5 = 3 + 20 = 23 Ответ: 23

---

Вариант 2. Задание 2

(из сборника ЕГЭ 2024 математика профиль Ященко И.В. 50 вариантов) На координатной плоскости изображены векторы a^➔ и b^➔ с целочисленными координатами. Найдите скалярное произведение a^➔ × b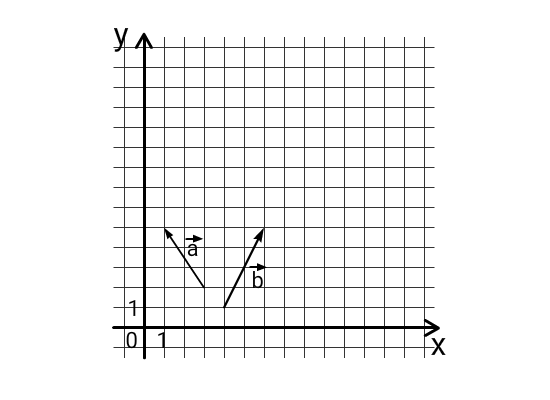^➔. Решение: 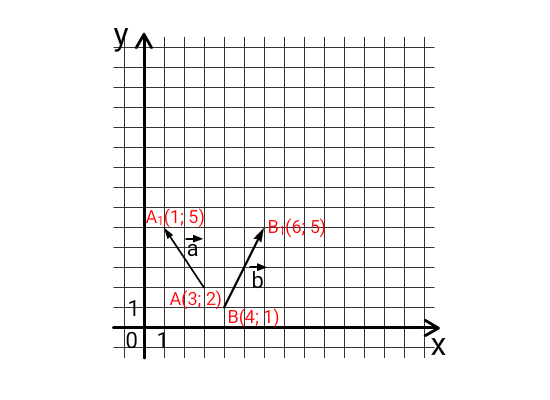По рисунку находим координаты начала и конца векторов: 1) a^➔ = AA₁^➔, где A(3; 2) — начало вектора,        A₁(1; 5) — конец вектора ⇒ AA₁^➔{1-3; 5-2} ⇒ AA₁^➔{-2; 3} 2) b^➔ = BB₁^➔, где B(4; 1) — начало вектора,        B₁(6; 5) — конец вектора ⇒ BB₁^➔{6-4; 5-1} ⇒ BB₁^➔{2; 4} 3) Найдем скалярное произведение векторов a^➔ × b^➔ = -2 × 2 + 3 × 4 = -4 + 12 = 8 Ответ: 8

---

Вариант 3. Задание 2

(из сборника ЕГЭ 2024 математика профиль Ященко И.В. 50 вариантов) На координатной плоскости изображены векторы a^➔ и b^➔ с целочисленными координатами. Найдите скалярное произведение a^➔ × b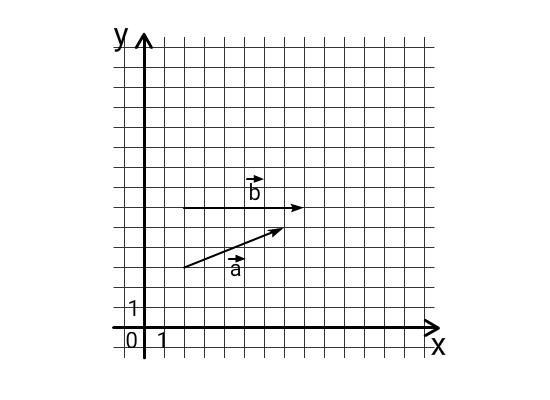^➔. Решение:

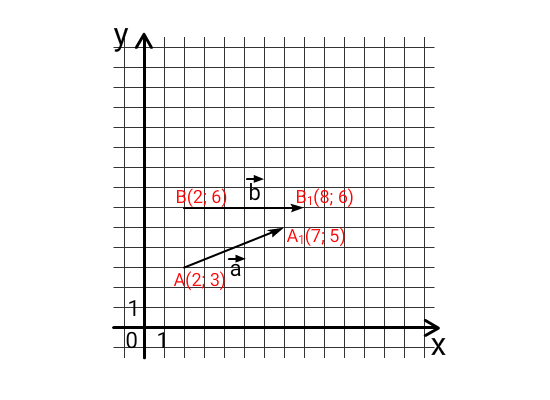
Вектор	Координаты начала	Координаты конца	Разность координат конца и начала вектора
a➔=AA1➔	A(2; 3)	A1(7; 5)	AA1➔{7-2; 5-3} = {5; 2}
b➔=BB1➔	B(2; 6)	B1(8; 6)	BB1➔{8-2; 6-6} = {6; 0}

Скалярное произведение векторов равно сумме произведений соответствующих координат вектора. a^➔ × b^➔ = 5 × 6 + 2 × 0 = 30

Ответ: 30