Часть 1
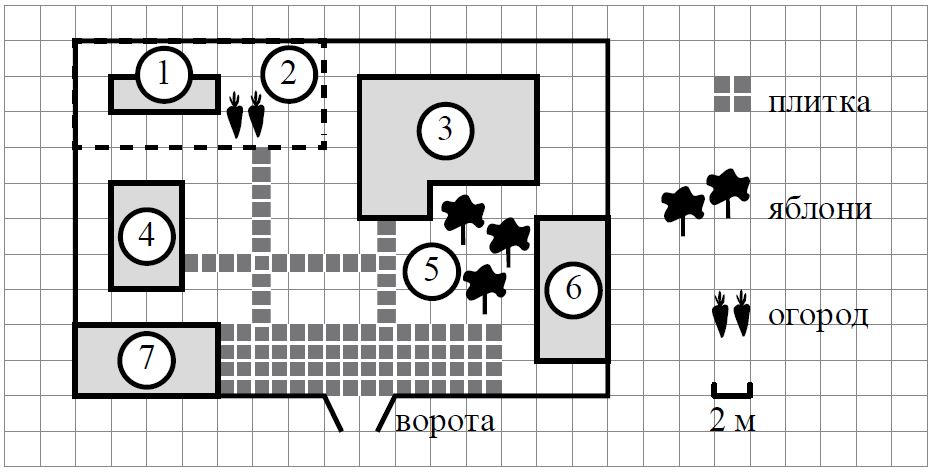
На плане изображено домохозяйство по адресу: с. Авдеево, 3-й Поперечный пер., д. 13 (сторона каждой клетки на плане равна 2 м).
Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок справа от ворот находится баня, а слева – гараж, отмеченный на плане цифрой 7. Площадь, занятая гаражом, равна 32 кв. м.
Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеется сарай (подсобное помещение), расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Перед жилым домом имеются яблоневые посадки.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м×1м . Между баней и гаражом имеется площадка
площадью 64 кв. м, вымощенная такой же плиткой.
К домохозяйству подведено электричество. Имеется магистральное газоснабжение.
Задание №1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите
последовательность четырёх цифр.
| Объекты |
Жилой дом |
Сарай |
Баня |
Теплица |
| Цифры |
|
|
|
|
Решение:
6 — баня
7 — гараж
3 — дом
4 — сарай
2 — огород
1 — теплица
5 — яблоня
| Объекты |
Жилой дом |
Сарай |
Баня |
Теплица |
| Цифры |
3 |
4 |
6 |
1 |
Ответ: 3461
Задание №2
Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок плитки понадобилось купить, чтобы выложить все дорожки и площадку перед гаражом?
Решение:
S
гаража = 32м
2
Плитка 1м × 1м
S
площадки = 64м
2
1 упаковка — 4 штуки (плитки)
? упаковок — все дорожки + площадка
На площадку — 64 плитки
На дорожки — 26 плиток
Всего потребуется 64 + 26 = 90 плиток
90 : 4 = 22.5 ⇒ 23 упаковки понадобилось
Ответ: 23
Задание №3
Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.
Решение:
S
дома — ? м
2
Дом содержит 17 клеток
S
1 клетки = 2м
2 × 2м
2 = 4 м
2
S
дома = 17 × 4 = 68 м
2
Ответ: 68
Задание №4
Найдите расстояние от жилого дома до гаража (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение:
S
от дома до гаража — ? м
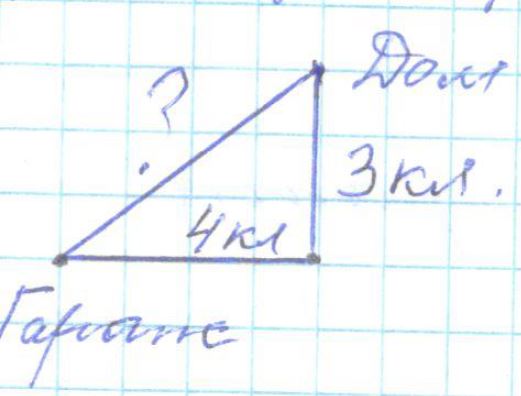
S = √
4² + 3² = 5 клеток
S = 5 клеток × 2 м = 10 м
Ответ: 10
Задание №5
Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
|
Нагреватель (котёл) |
Прочее оборудование и монтаж |
Сред. расход газа / сред. потребл. мощность |
Стоимость газа / электроэнергии |
| Газовое отопление |
24 тыс. руб. |
18280 руб. |
1,2 куб. м/ч |
5,6 руб./куб. м |
| Электр. отопление |
20 тыс. руб. |
15000 руб. |
5,6 кВт |
3,8 руб./(кВт ⋅ ч) |
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия
от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического отопления?
Решение:
1) Газ (по таблице) 24000 руб + 18280 руб = 42280 руб.
1.2 м³/ч × 5.6 руб/м³ = 6.72 руб.
2) Электричество (по таблице)
20000 руб + 15000 руб = 35000 руб
5.6 кВт × 3.8 руб/кВт⋅ч = 21.28 руб
3) Разница в 42280 руб — 35000 руб = 7280 руб оборудование
21.28 руб — 6,72 руб = 14.56 руб к оплате
7280 : 14.56 = 500 (ч) экономия
Ответ: 500
Задание №6
Найдите значение выражения
56 —
314. Представьте результат в виде несократимой обыкновенной дроби. В ответ запишите числитель этой дроби.
Решение:
56 —
314 =
35 — 942 =
2642 =
1321
Ответ: 13
Задание №7
На координатной прямой отмечена точка А.
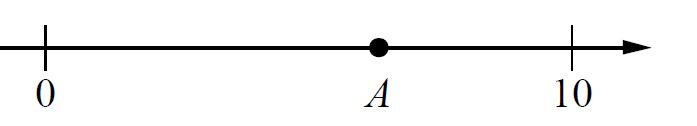
Известно, что она соответствует одному из четырёх указанных ниже чисел.
Какому из чисел соответствует точка А?
1)
18116
2) √
37
3) 0.6
4) 4
Решение:
1)
18116 = 11
516 > 10 ⇒ не точка A
2) 6 < √
37 < 7 ⇒ точка A
Ответ: 2
Задание №8
Найдите значение выражения a
-7 × (a
5)
2 при a = 5.
Решение:
a
-7 × (a
5)
2 = a
-7 × a
10 = a
-7 + 10 = a
3
при a = 5
5
3 = 5 × 5 × 5 = 125
Ответ: 125
Задание №9
Решите уравнение x
2 + x − 12 = 0.
Если уравнение имеет более одного корня, в ответ запишите больший из корней.
Решение:
x
2 + x − 12 = 0 по теореме Виета

x
1 + x
2 = -1
x
1 × x
2 = -12
Подбором

-4 + 3 = -1
-4 × 3 = -12
x
1 = -4 x
2 = 3 — больший корень системы уравнений
Ответ: 3
Задание №10
На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.
Решение:
С мясом — 4 шт.
С капустой — 8 шт.
С яблоком — 3шт.
P
с яблоком =
34 + 8 + 3 =
315 =
15 = 0.2
Ответ: 0.2
Задание №1
Установите соответствие между графиками функций и формулами, которые их задают.
Графики
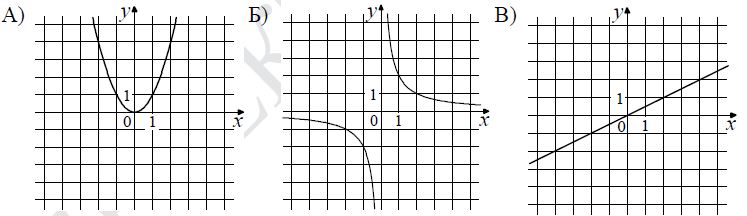
Формулы
1) y = x
2
2) y =
x2
3) y =
2x
В таблице под каждой буквой укажите соответствующий номер.
Решение:
А) парабола ⇒ 1) y = x
2
Б) гипербола ⇒ 3) y =
2x
В) прямая ⇒ 2) y =
x2 =
12x
Ответ: 132
Задание №12
Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой t
F =1,8t
C + 32, где t
C – температура в градусах Цельсия, t
F – температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует −25 градусов по шкале Цельсия?
Решение:
t
F = 1.8t
c + 32 t
c= -25° t
F — ?
t
F = 1.8 × (-25) + 32 = -45 + 32 = -13
Ответ: -13
Задание №13
Укажите решение системы неравенств

x + 2.6 ≤ 0
x + 5 ≥ 1
 Решение:
Решение:

x + 2.6 ≤ 0
x + 5 ≥ 1

x ≤ -2.6
x ≥ 1 — 5

x ≤ -2.6
x ≥ -4
2) [-4; -2.6]
Ответ: 2
Задание №14
Вика решила начать делать зарядку каждое утро. В первый день она сделала 30 приседаний, а в каждый следующий день она делала на одно и то же количество приседаний больше, чем в предыдущий день. За 15 дней она сделала всего 975 приседаний. Сколько приседаний сделала Вика на пятый день?
Решение:
(a
n) — арифметическая прогрессия
a
1 = 30 S
15 = 975 a
5 — ?
1) S
n =
2a1 + d(n — 1)2 × n
975 =
2 × 30 + d(15 — 1)2 × 15 | :15
65 =
60 + 14d2 | ×2
130 = 60 + 14d
14d = 130 — 60 = 70
d = 70 : 14 = 5
2) a
5 = a
1 + d × (n — 1)
a
5 = 30 + 5 × (5 — 1)
a
5 = 30 + 5 × 4 = 30 + 20
a
5 = 50
Ответ: 50
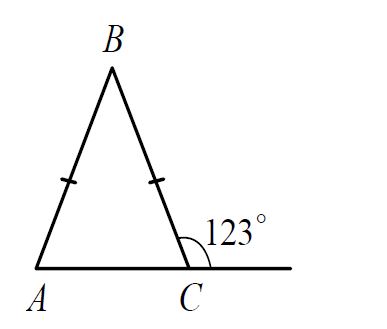
Задание №15
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ВАС. Ответ дайте в градусах.
 Решение:
Решение:
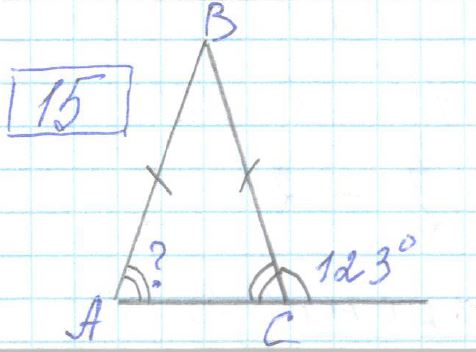
1) ∠ A = ∠ C (углы при основании AC)
2) ∠ C = 180° — 123° = 57° (смежные углы)
Ответ: 57
Задание №16
Найдите длину хорды окружности радиусом 13, если расстояние от центра окружности до хорды равно 5.
 Решение:
Решение:
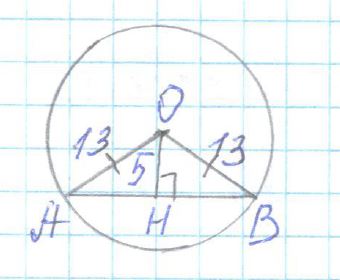
R = 13 h = 5 AB — ?
1) Δ AOH (∠ H = 90°)
AH = √
13² — 5² = 12 по теореме Пифагора
2) AB = 2AH = 2 — 12 = 24
Свойство высоты равнобедренного треугольника.
Ответ: 24
Задание №17
Найдите площадь трапеции, изображённой на рисунке.
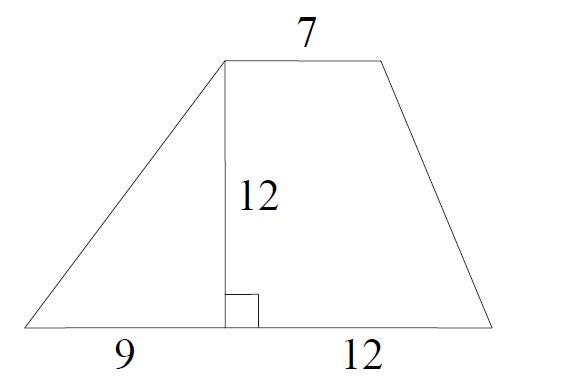 Решение:
Решение:
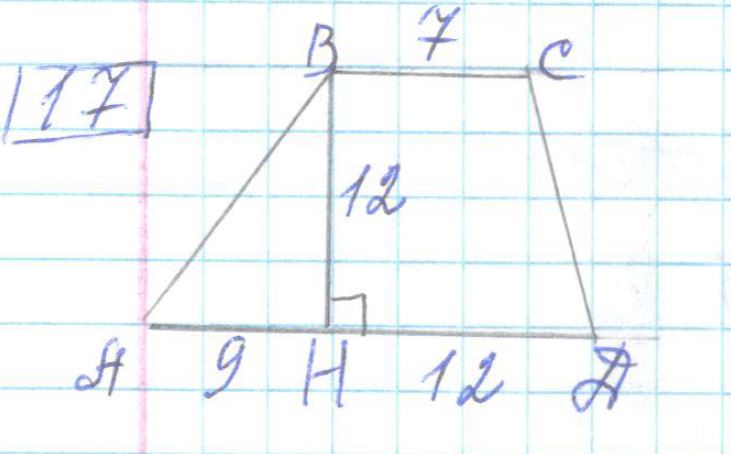
S
трапеции — ?
S =
AD + BC2 × BH
S =
(9 + 12) + 72 × 12
S =
282 × 12 = 14 × 12 = 168
Ответ: 168
Задание №18
Найдите тангенс острого угла, изображённого на рисунке.
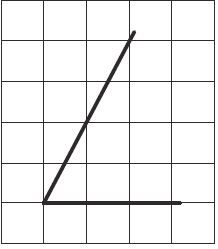 Решение:
Решение:
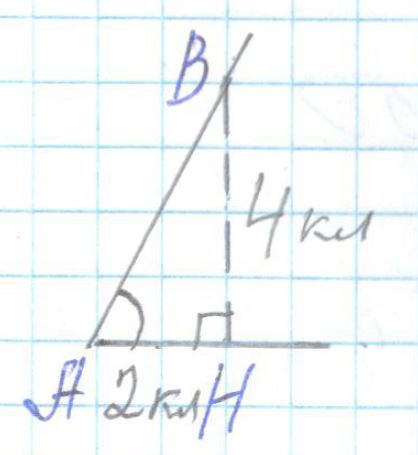
tg BAH — ?
BH ⊥ AH
Δ ABH (∠ H = 90°)
tg A =
BHAH =
42 = 2
Ответ: 2
Задание №19
Какие из следующих утверждений верны?
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) В любом параллелограмме есть два равных угла.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Решение:
1)
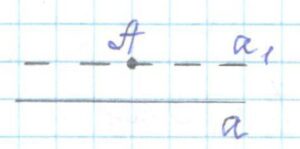
A ∉ a a || a
1 верно
2) a = 1 b = 2 c = 4
4 < 1 + 2
4 < 3 неравенство треугольников неверно
3)

∠ A = ∠ C
∠ B = ∠ D верно
Ответ: 13
Часть 2. Задание №1
Решите уравнение
x
4 = (4x − 5)
2
Решение:
x
4 = (4x — 5)
2
(x
2)
2 — (4x — 5)
2 = 0
(x
2 — (4x — 5))(x
2 + (4x — 5)) = 0
(x
2 — 4x + 5)(x
2 + 4x — 5) = 0
x
2 — 4x + 5 = 0
D = 16 — 20 < 0 нет корней
или x
2 + 4x — 5 = 0
по теореме Виета
x
1 = -5 x
2 = 1
Ответ: -5; 1
Задание №21
Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отплыл, если скорость течения реки равна 2 км/ч,
а собственная скорость лодки равна 6 км/ч?
Решение:
|
V км/ч |
t ч |
S км |
| по течению |
6 + 2 = 8 |
x8 |
x |
| против течения |
6 — 2 = 4 |
x4 |
x |
t
по течению + t
против течения = (10ч — 5ч) — 2ч = 3ч
x8 +
x4 = 3 | ×8
x + 2x = 24
3x = 24
x = 24 : 3 = 8
Значит, 8 км отплыл от пристани.
Ответ: 8
Задание №22
Постройте график функции
y =
x4 — 13x2 + 36(x — 3)(x + 2)
и определите, при каких значениях с прямая y =c имеет с графиком ровно одну общую точку.
Решение:
y =
x4 — 13x2 + 36(x — 3)(x + 2) c — ? y = c одна общая точка
1) Разложим числитель на множители (x
2)
2 — 13x
2 + 36
Пусть x
2 = t, тогда t
2 — 13t + 36
D = 169 — 4 × 36 = 169 — 144 = 25
t
1 =
13 — 52 = 4
t
2 =
13 + 52 = 9
t
2 — 13t + 36 = (t — 4)(t — 9) = (x
2 — 4)(x
2 — 9) = (x — 2)(x + 2)(x — 3)(x + 3)
2) Преобразуем (дробь) функцию
y =
(x — 2)(x + 2)(x — 3)(x + 3)(x — 3)(x + 2)
x ≠ -2
x ≠ 3
y = (x — 2)(x + 3) = x
2 — 2x + 3x — 6
y = x
2 + x — 6
3) Построим график
x
0 = —
b2a = —
12
y
0 = (-
12)
2 —
12 — 6
y
0 = -6.25
(-0.5; -6.25) вершина параболы
Найдём точки пересечения с OX: y = 0
x
2 + x — 6 = 0
x
1 = -3
x
2 = 2
(-3; 0) и (2; 0)
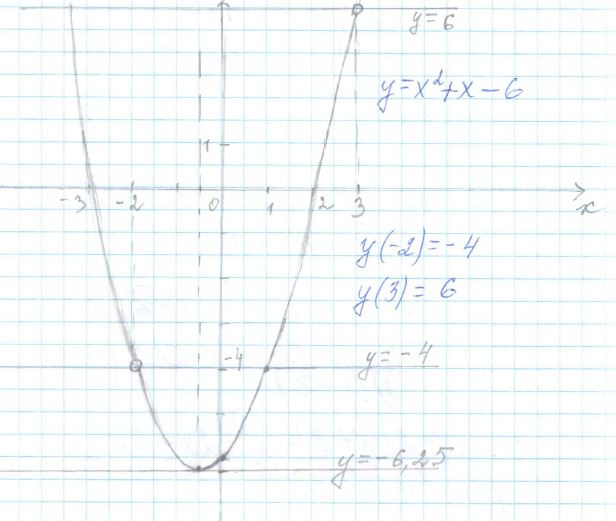 Ответ:
Ответ: при c = -6.25
c = -4
c = 6
прямая y = c имеет с графиком ровно одну общую точку.
Задание №23
В прямоугольном треугольнике ABC с прямым углом C известны катеты:
AC = 6, BC=8. Найдите медиану CK этого треугольника.
Решение:
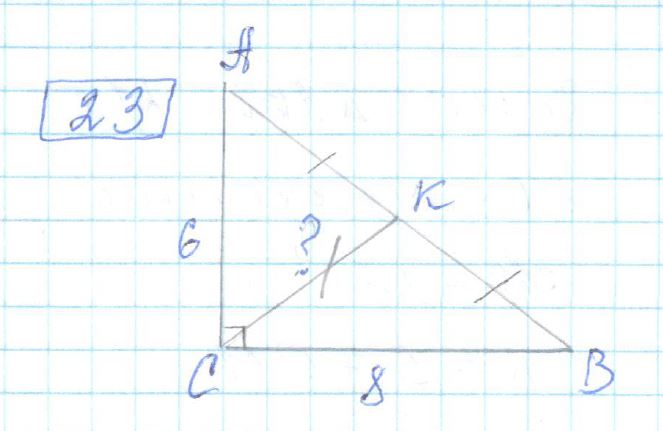
1) CK =
12AB = AK = KB
2) AB = √
6² + 8²
AB = √
100 = 10
3) CK =
12 × 10 = 5
Ответ: 5
Задание №24
В параллелограмме ABCD точка E – середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм – прямоугольник.
Решение:
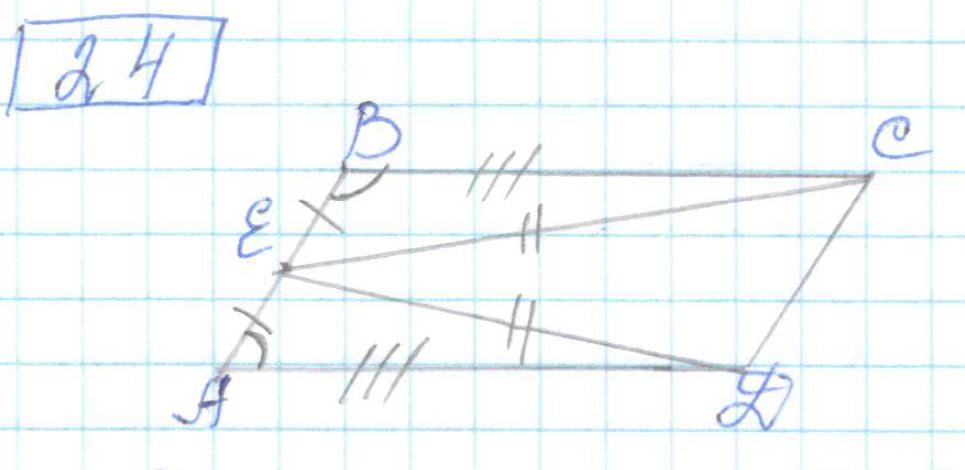
Доказать, что ABCD — прямоугольник.
Доказательство:
1) Δ ADE = Δ CBE (равны по трем сторонам)
2) ∠ DAE = ∠ CBE (из равенства треугольников)
3) ∠ A + ∠ B = 180° (свойство параллелограмма)
4) ∠ A = ∠ B = 180° : 2 = 90° ⇒ ABCD — прямоугольник, что и требовалось доказать.
Ответ: ABCD — прямоугольник
Задание №25
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиусом 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC. Найдите радиус окружности, вписанной в треугольник ABC.
Решение:
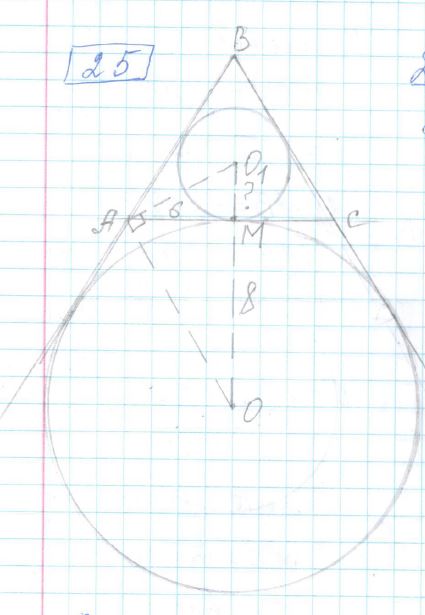
Дано: Δ ABC — равнобедренный
AC — основание
AC = 12
R = 8 = OM
Найти: r = O
1M
1) M — середина AC ⇒ AM = MC = 6
2) O ∈ биссектрисе AO, O
1 ∈ биссектрисе AO
1
AO ∩ AO
1 = A, ∠ OAO
1 = 90°
3) Δ AOO
1, ∠ A = 90° AM — высота ⇒ AM = √
MO₁ × MO
AM
2 = MO
1 × MO
6
2 = MO
1 × 8
MO
1 =
368 = 4.5
Ответ: 4.5
Задания взяты из демонстрационного варианта ОГЭ по математике 2024 с сайта ФИПИ https://fipi.ru/oge/demoversii-specifikacii-kodifikatory#!/tab/173801626-2
Файлы для скачивания:
 На плане изображено домохозяйство по адресу: с. Авдеево, 3-й Поперечный пер., д. 13 (сторона каждой клетки на плане равна 2 м).
Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок справа от ворот находится баня, а слева – гараж, отмеченный на плане цифрой 7. Площадь, занятая гаражом, равна 32 кв. м.
Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеется сарай (подсобное помещение), расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Перед жилым домом имеются яблоневые посадки.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м×1м . Между баней и гаражом имеется площадка
площадью 64 кв. м, вымощенная такой же плиткой.
К домохозяйству подведено электричество. Имеется магистральное газоснабжение.
На плане изображено домохозяйство по адресу: с. Авдеево, 3-й Поперечный пер., д. 13 (сторона каждой клетки на плане равна 2 м).
Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок справа от ворот находится баня, а слева – гараж, отмеченный на плане цифрой 7. Площадь, занятая гаражом, равна 32 кв. м.
Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеется сарай (подсобное помещение), расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Перед жилым домом имеются яблоневые посадки.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м×1м . Между баней и гаражом имеется площадка
площадью 64 кв. м, вымощенная такой же плиткой.
К домохозяйству подведено электричество. Имеется магистральное газоснабжение.
 S = √4² + 3² = 5 клеток
S = 5 клеток × 2 м = 10 м
Ответ: 10
S = √4² + 3² = 5 клеток
S = 5 клеток × 2 м = 10 м
Ответ: 10
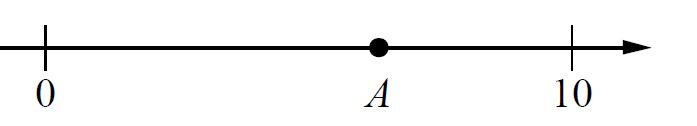 Известно, что она соответствует одному из четырёх указанных ниже чисел.
Какому из чисел соответствует точка А?
1) 18116
2) √37
3) 0.6
4) 4
Решение:
1) 18116 = 11516 > 10 ⇒ не точка A
2) 6 < √37 < 7 ⇒ точка A
Ответ: 2
Известно, что она соответствует одному из четырёх указанных ниже чисел.
Какому из чисел соответствует точка А?
1) 18116
2) √37
3) 0.6
4) 4
Решение:
1) 18116 = 11516 > 10 ⇒ не точка A
2) 6 < √37 < 7 ⇒ точка A
Ответ: 2
 Формулы
1) y = x2
2) y = x2
3) y = 2x
В таблице под каждой буквой укажите соответствующий номер.
Формулы
1) y = x2
2) y = x2
3) y = 2x
В таблице под каждой буквой укажите соответствующий номер.
 Решение:
Решение:
 Решение:
Решение:
 1) ∠ A = ∠ C (углы при основании AC)
2) ∠ C = 180° — 123° = 57° (смежные углы)
Ответ: 57
1) ∠ A = ∠ C (углы при основании AC)
2) ∠ C = 180° — 123° = 57° (смежные углы)
Ответ: 57
 Решение:
Решение:
 R = 13 h = 5 AB — ?
1) Δ AOH (∠ H = 90°)
AH = √13² — 5² = 12 по теореме Пифагора
2) AB = 2AH = 2 — 12 = 24
Свойство высоты равнобедренного треугольника.
Ответ: 24
R = 13 h = 5 AB — ?
1) Δ AOH (∠ H = 90°)
AH = √13² — 5² = 12 по теореме Пифагора
2) AB = 2AH = 2 — 12 = 24
Свойство высоты равнобедренного треугольника.
Ответ: 24
 Решение:
Решение:
 S трапеции — ?
S = AD + BC2 × BH
S = (9 + 12) + 72 × 12
S = 282 × 12 = 14 × 12 = 168
Ответ: 168
S трапеции — ?
S = AD + BC2 × BH
S = (9 + 12) + 72 × 12
S = 282 × 12 = 14 × 12 = 168
Ответ: 168
 Решение:
Решение:
 tg BAH — ?
BH ⊥ AH
Δ ABH (∠ H = 90°)
tg A = BHAH = 42 = 2
Ответ: 2
tg BAH — ?
BH ⊥ AH
Δ ABH (∠ H = 90°)
tg A = BHAH = 42 = 2
Ответ: 2
 A ∉ a a || a1 верно
2) a = 1 b = 2 c = 4
4 < 1 + 2
4 < 3 неравенство треугольников неверно
3)
A ∉ a a || a1 верно
2) a = 1 b = 2 c = 4
4 < 1 + 2
4 < 3 неравенство треугольников неверно
3)  ∠ A = ∠ C
∠ B = ∠ D верно
Ответ: 13
∠ A = ∠ C
∠ B = ∠ D верно
Ответ: 13
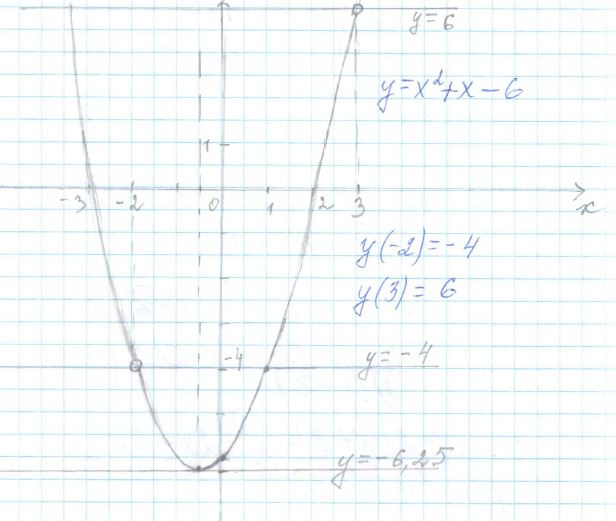 Ответ: при c = -6.25
c = -4
c = 6
прямая y = c имеет с графиком ровно одну общую точку.
Ответ: при c = -6.25
c = -4
c = 6
прямая y = c имеет с графиком ровно одну общую точку.
 1) CK = 12AB = AK = KB
2) AB = √6² + 8²
AB = √100 = 10
3) CK = 12 × 10 = 5
Ответ: 5
1) CK = 12AB = AK = KB
2) AB = √6² + 8²
AB = √100 = 10
3) CK = 12 × 10 = 5
Ответ: 5
 Доказать, что ABCD — прямоугольник.
Доказательство:
1) Δ ADE = Δ CBE (равны по трем сторонам)
2) ∠ DAE = ∠ CBE (из равенства треугольников)
3) ∠ A + ∠ B = 180° (свойство параллелограмма)
4) ∠ A = ∠ B = 180° : 2 = 90° ⇒ ABCD — прямоугольник, что и требовалось доказать.
Ответ: ABCD — прямоугольник
Доказать, что ABCD — прямоугольник.
Доказательство:
1) Δ ADE = Δ CBE (равны по трем сторонам)
2) ∠ DAE = ∠ CBE (из равенства треугольников)
3) ∠ A + ∠ B = 180° (свойство параллелограмма)
4) ∠ A = ∠ B = 180° : 2 = 90° ⇒ ABCD — прямоугольник, что и требовалось доказать.
Ответ: ABCD — прямоугольник
 Дано: Δ ABC — равнобедренный
AC — основание
AC = 12
R = 8 = OM
Найти: r = O1M
1) M — середина AC ⇒ AM = MC = 6
2) O ∈ биссектрисе AO, O1 ∈ биссектрисе AO1
AO ∩ AO1 = A, ∠ OAO1 = 90°
3) Δ AOO1, ∠ A = 90° AM — высота ⇒ AM = √MO₁ × MO
AM2 = MO1 × MO
62 = MO1 × 8
MO1 = 368 = 4.5
Ответ: 4.5
Дано: Δ ABC — равнобедренный
AC — основание
AC = 12
R = 8 = OM
Найти: r = O1M
1) M — середина AC ⇒ AM = MC = 6
2) O ∈ биссектрисе AO, O1 ∈ биссектрисе AO1
AO ∩ AO1 = A, ∠ OAO1 = 90°
3) Δ AOO1, ∠ A = 90° AM — высота ⇒ AM = √MO₁ × MO
AM2 = MO1 × MO
62 = MO1 × 8
MO1 = 368 = 4.5
Ответ: 4.5





