Задание 1 (пример 1)
Текст задачи:Шоколадка стоит 25 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за три шоколадки, покупатель получает четыре (одну в подарок). Сколько шоколадок можно получить на 130 рублей в воскресенье?
Решение: Ответ:
Ответ:
Задание 1 (пример 2)
Текст задачи:Стоимость проездного билета на месяц составляет 580 рублей, а стоимость билета на одну поездку 20 рублей. Аня купила проездной и сделала за месяц 41 поездку. На сколько рублей больше она бы потратила, если бы покупала билеты на одну поездку?
Решение: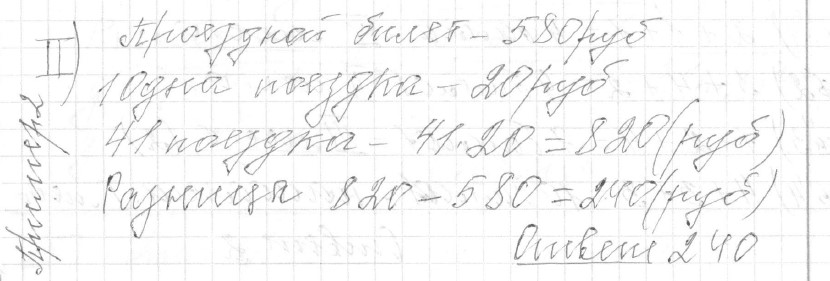 Ответ:
Ответ:
Задание 1 (пример 3)
Текст задачи:Для покраски 1 кв. м потолка требуется 200 г краски. Краска продаётся в банках по 2 кг. Какой наименьшее количество банок краски нужно для покраски потолка площадью 64 ?
Решение: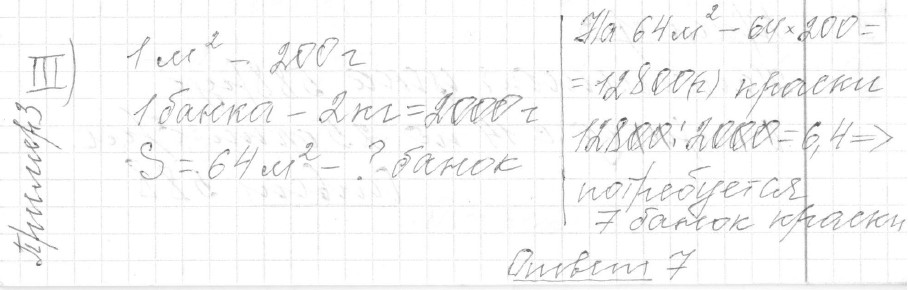 Ответ:
Ответ:
Задание 2 (пример 1)
Текст задачи:Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ЗНАЧЕНИЯ |
|---|---|
| А) рост жирафа | 1) 6400 км |
| Б) толщина лезвия бритвы | 2) 500 см |
| В) радиус Земли | 3) 0,08 мм |
| Г) ширина футбольного поля | 4) 68 м |
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Решение: Ответ:
Ответ:
Задание 2 (пример 2)
Текст задачи:Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ЗНАЧЕНИЯ |
|---|---|
| А) масса новорождённого ребёнка | 1) 3500 г |
| Б) масса кухонного холодильника | 2) 18 т |
| В) масса карандаша | 3) 15 г |
| Г) масса автобуса | 4) 38 кг |
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Решение: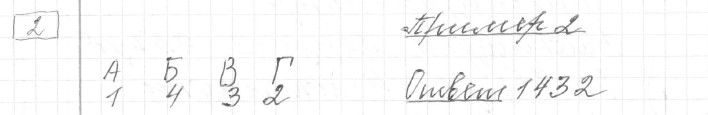 Ответ:
Ответ:
Задание 3 (пример 1)
Текст задачи:На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия.
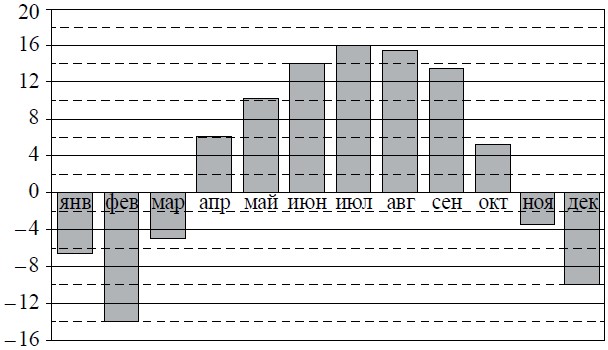
Определите по диаграмме наименьшую среднемесячную температуру в Нижнем Новгороде в 1994 году. Ответ дайте в градусах Цельсия.
Решение: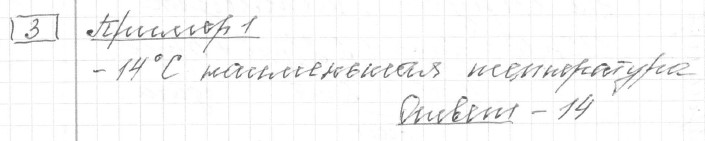 Ответ:
Ответ:
Задание 3 (пример 2)
Текст задачи:В нескольких эстафетах, которые проводились в школе, команды показали следующие результаты:
| Команда | I эстафета, баллы | II эстафета, баллы | III эстафета, баллы |
|---|---|---|---|
| «Непобедимые» | 2 | 1 | 1 |
| «Прорыв» | 3 | 4 | 2 |
| «Чемпионы» | 1 | 2 | 4 |
| «Тайфун» | 4 | 3 | 3 |
При подведении итогов для каждой команды баллы по всем эстафетам суммируются. Побеждает команда, набравшая наибольшее количество баллов. Какое итоговое место заняла команда «Чемпионы»?
Решение: Ответ:
Ответ:
Задание 3 (пример 3)
Текст задачи:На рисунке жирными точками показана цена палладия, установленная Центробанком РФ на все рабочие дни в октябре 2010 года. По горизонтали указаны числа месяца, по вертикали — цена палладия в рублях за грамм. Для наглядности жирные точки на рисунке соединены линиями.
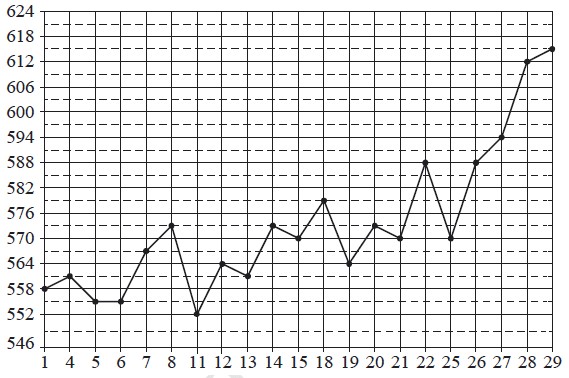
Определите по рисунку наибольшую цену палладия в период с 14 по 25 октября включительно. Ответ дайте в рублях за грамм.
Решение: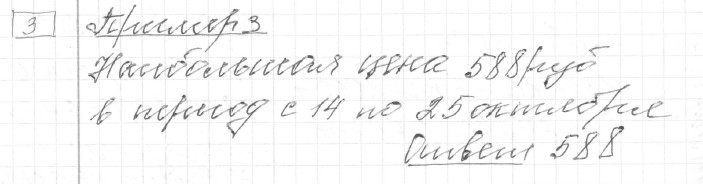 Ответ:
Ответ:
Задание 4 (пример 1)
Текст задачи:Работа постоянного тока (в джоулях) вычисляется по формуле , где U — напряжение (в вольтах), R — сопротивление (в омах), t — время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если .
Решение: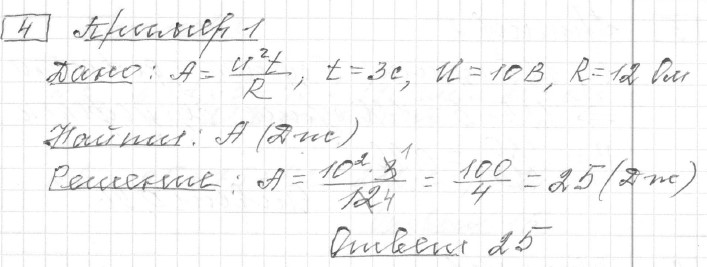 Ответ:
Ответ:
Задание 4 (пример 2)
Текст задачи:Среднее геометрическое трёх чисел: a, b и c — вычисляется по формуле . Вычислите среднее геометрическое чисел 5, 25 и 27.
Решение: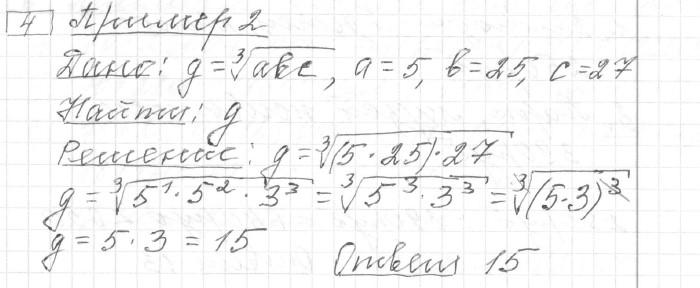 Ответ:
Ответ:
Задание 5 (пример 1)
Текст задачи:Научная конференция проводится в 4 дня. Всего запланировано 60 докладов: первые два дня — по 12 докладов, остальные распределены поровну между третьим и четвёртым днями. На конференции планируется доклад профессора М. Порядок докладов определяется случайным образом. Какова вероятность того, что доклад профессора М. окажется запланированным на последний день конференции?
Решение: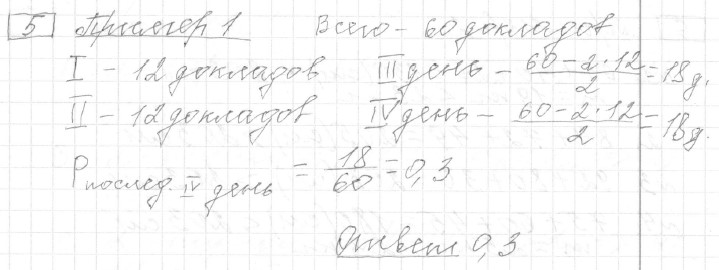 Ответ:
Ответ:
Задание 5 (пример 2)
Текст задачи:Фабрика выпускает сумки. В среднем из 125 сумок, поступивших в продажу, 5 сумок имеют скрытый дефект. Найдите вероятность того, что случайно выбранная сумка окажется без дефекта.
Решение: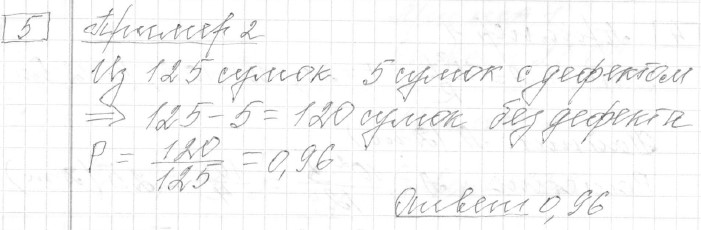 Ответ:
Ответ:
Задание 6 (пример 1)
Текст задачи:Турист подбирает экскурсии. Сведения об экскурсиях представлены в таблице.
| Номер экскурсии | Посещаемые объекты | Стоимость (руб.) |
|---|---|---|
| 1 | Загородный дворец, крепость | 250 |
| 2 | Крепость | 100 |
| 3 | Парк, музей живописи | 390 |
| 4 | Загородный дворец | 200 |
| 5 | Музей живописи | 150 |
| 6 | Загородный дворец, парк | 320 |
Пользуясь таблицей, подберите набор экскурсий так, чтобы турист посетил четыре объекта: крепость, загородный дворец, парк и музей живописи, а суммарная стоимость экскурсий не превышала 650 рублей.
В ответе запишите какой-нибудь один набор номеров экскурсий без пробелов, запятых и других дополнительных символов.
Решение: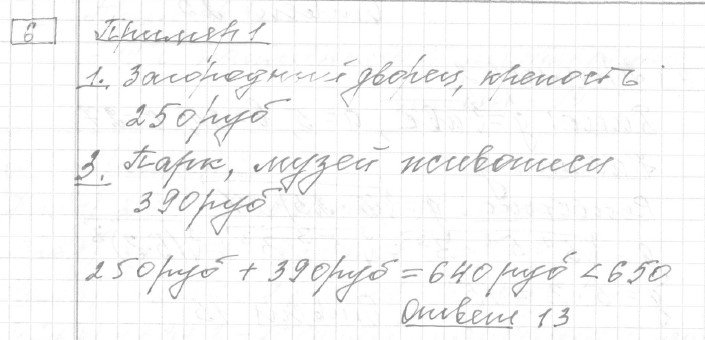 Ответ:
Ответ:
Задание 6 (пример 2)
Текст задачи:В таблице приведены данные о шести чемоданах.
| Номер чемодана | Длина (см) | Высота (см) | Ширина (см) | Масса (кг) |
|---|---|---|---|---|
| 1 | 65 | 40 | 25 | 19 |
| 2 | 84 | 72 | 49 | 24 |
| 3 | 92 | 80 | 36 | 23 |
| 4 | 75 | 60 | 45 | 25 |
| 5 | 83 | 65 | 48 | 22,5 |
| 6 | 95 | 75 | 42 | 30 |
По правилам авиакомпании сумма трёх измерений (длина, высота, ширина) чемодана, сдаваемого в багаж, не должна превышать 203 см, а масса не должна быть больше 23 кг. Какие чемоданы можно сдать в багаж по правилам этой авиакомпании?
В ответе укажите номера всех выбранных чемоданов (без пробелов, запятых и других дополнительных символов).
Решение: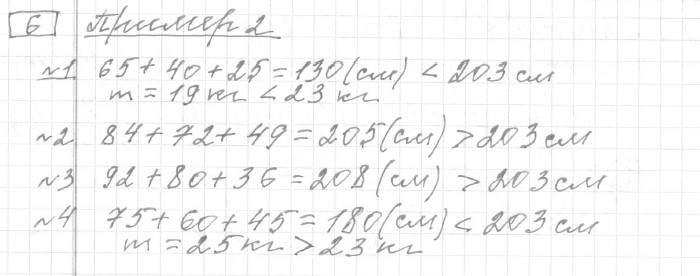
 Ответ:
Ответ:
Задание 6 (пример 3)
Текст задачи:Строительная фирма планирует купить 70 пеноблоков у одного из трёх поставщиков. Цены и условия доставки приведены в таблице.
| Поставщик | Стоимость пеноблоков (руб. за 1 ) | Стоимость доставки (руб.) | Дополнительные условия |
|---|---|---|---|
| А | 2600 | 10000 | Нет |
| Б | 2800 | 8000 | При заказе товара на сумму свыше 150000 рублей доставка бесплатная |
| В | 2700 | 8000 | При заказе товара на сумму свыше 200000 рублей доставка бесплатная |
Сколько рублей нужно заплатить за самую дешёвую покупку с доставкой?
Решение: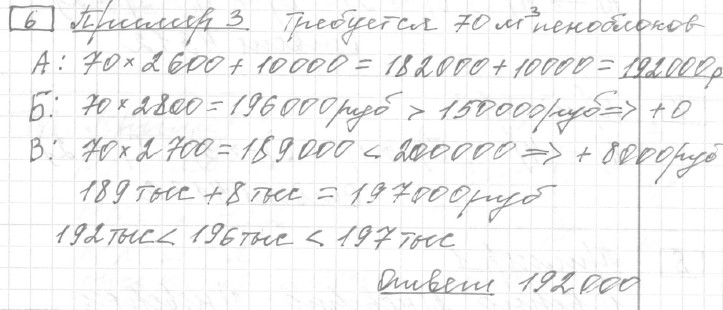 Ответ:
Ответ:
Задание 7 (пример 1)
Текст задачи:На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
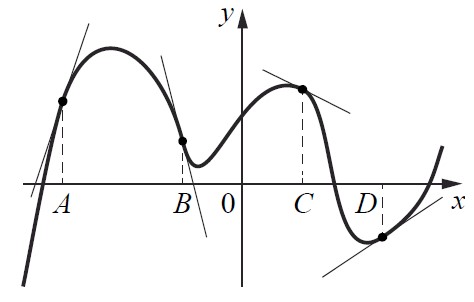
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
|---|---|
| A | |
| B | |
| C | |
| D |
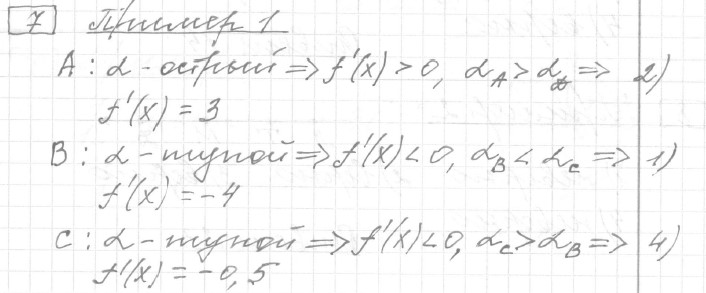
 Ответ:
Ответ:
Задание 7 (пример 2)
Текст задачи:На графике изображена зависимость крутящего момента двигателя от числа оборотов в минуту. На горизонтальной оси отмечено число оборотов в минуту, на вертикальной оси — крутящий момент в Н·м.
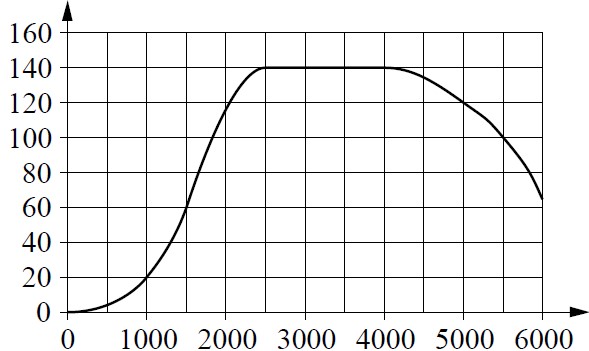
Пользуясь графиком, поставьте в соответствие каждому интервалу числа оборотов в минуту характеристику крутящего момента на этом интервале.
| ИНТЕРВАЛЫ | ХАРАКТЕРИСТИКИ |
|---|---|
| А) 0–500 об./мин. | 1) при увеличении числа оборотов крутящий момент не меняется |
| Б) 1000–2500 об./мин. | 2) при увеличении числа оборотов крутящий момент уменьшается |
| В) 2500–4000 об./мин. | 3) при увеличении числа оборотов самый быстрый рост крутящего момента |
| Г) 4000–6000 об./мин. | 4) при увеличении числа оборотов крутящий момент не превышает 20 Н·м. |
 Ответ:
Ответ:
Задание 7 (пример 3)
Текст задачи:Установите соответствие между графиками функций и характеристиками этих функций на отрезке .
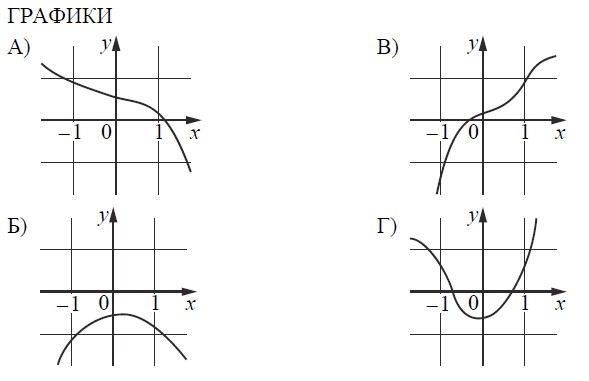
ХАРАКТЕРИСТИКИ
- Функция имеет точку максимума на отрезке
- Функция имеет точку минимума на отрезке
- Функция возрастает на отрезке
- Функция убывает на отрезке
В таблице под каждой буквой укажите соответствующий номер.
Решение: Ответ:
Ответ:
Задание 8 (пример 1)
Текст задачи:Кондитер испёк 40 печений, из них 10 штук он посыпал корицей, а 20 штук он собирается посыпать сахаром (кондитер может посыпать одно печенье и корицей, и сахаром, а может вообще ничем не посыпать). Выберите утверждения, которые будут верны при указанных условиях вне зависимости от того, какие печения кондитер посыплет сахаром.
- Найдётся 7 печений, которые ничем не посыпаны.
- Найдётся 8 печений, посыпанных и сахаром, и корицей.
- Если печенье посыпано корицей, то оно посыпано и сахаром.
- Не может оказаться 12 печений, посыпанных и сахаром, и корицей.
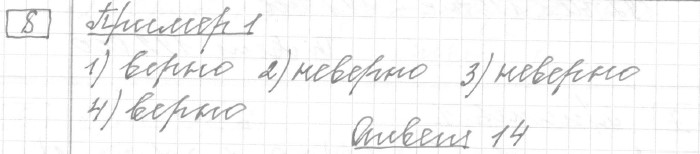 Ответ:
Ответ:
Задание 8 (пример 2)
Текст задачи:В доме Димы больше этажей, чем в доме Маши, в доме Лены меньше этажей, чем в доме Маши, а в доме Толи больше этажей, чем в Ленином доме. Выберите все утверждения, которые верны при указанных условиях.
- Среди этих четырёх домов есть три дома с одинаковым числом этажей.
- В Димином доме больше этажей, чем в Ленином.
- Дом Лены — самый малоэтажный среди перечисленных четырёх.
- В доме Маши меньше этажей, чем в доме Лены.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Решение: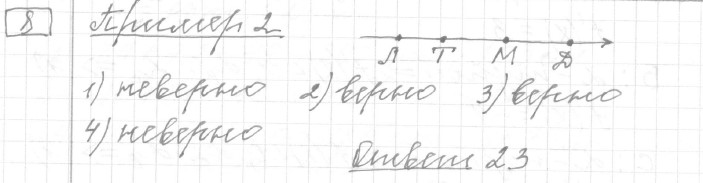 Ответ:
Ответ:
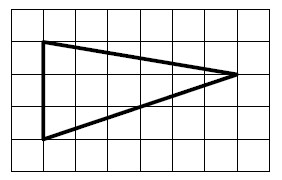
Задание 9 (пример 1)
Текст задачи:На рисунке изображён план местности (шаг сетки плана соответствует расстоянию 1 км на местности). Оцените, скольким квадратным километрам равна площадь озера Великое, изображённого на плане. Ответ округлите до целого числа.
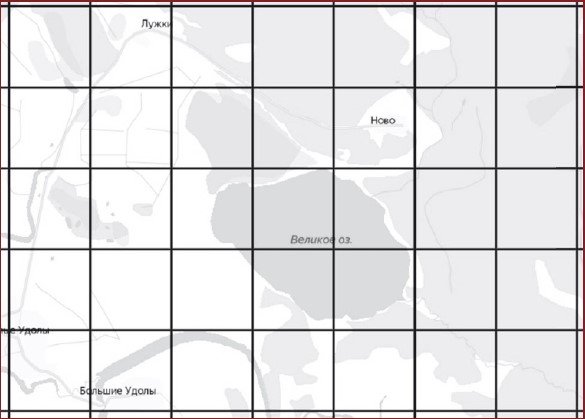 Решение:
Решение:
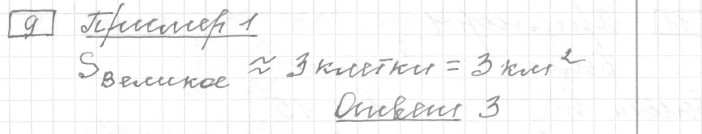 Ответ:
Ответ:
Задание 9 (пример 2)
Текст задачи:План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
 Решение:
Решение:
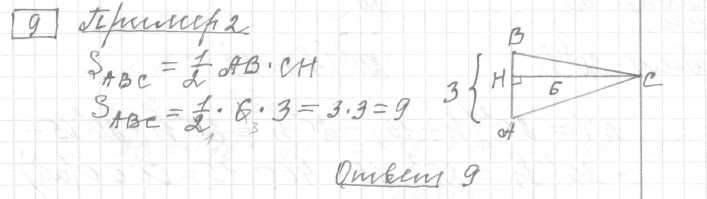 Ответ:
Ответ:
Задание 10 (пример 1)
Текст задачи:Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту этого столба, если наименьшая высота перил равна 0,8 м, а наибольшая высота равна 1,6 м. Ответ дайте в метрах.
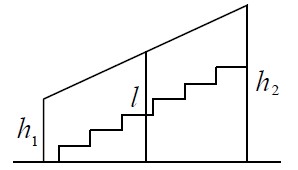 Решение:
Решение:
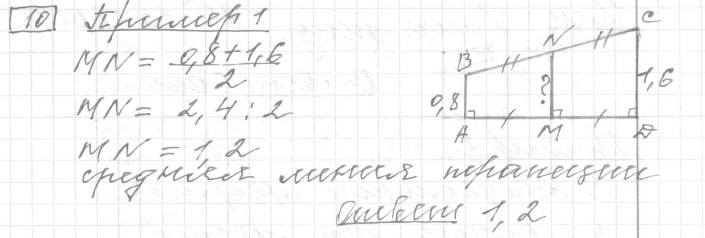 Ответ:
Ответ:
Задание 10 (пример 2)
Текст задачи:Какой угол (в градусах) образуют минутная и часовая стрелки в 16:00?
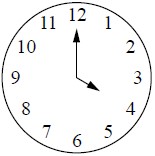 Решение:
Решение:
 Ответ:
Ответ:
Задание 11 (пример 1)
Текст задачи:В бак, имеющий форму правильной четырёхугольной призмы со стороной основания 20 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 15 см. Ответ дайте в кубических сантиметрах.
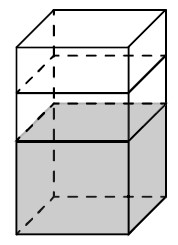 Решение:
Решение:
 Ответ:
Ответ:
Задание 11 (пример 2)
Текст задачи:От деревянной правильной треугольной призмы отпилили все вершины (см. рисунок). Сколько вершин у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
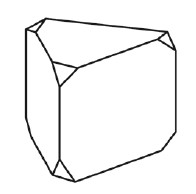 Решение:
Решение:
 Ответ:
Ответ:
Задание 12
Текст задачи:В треугольнике ABC медиана BM перпендикулярна стороне AC. Найдите длину стороны AB, если .
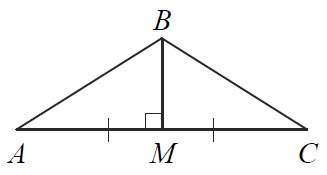 Решение:
Решение:
 Ответ:
Ответ:
Задание 13 (пример 1)
Текст задачи:Через точку, делящую высоту конуса в отношении 1 : 2, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём этого конуса, если объём конуса, отсекаемого от данного конуса проведённой плоскостью, равен 10.
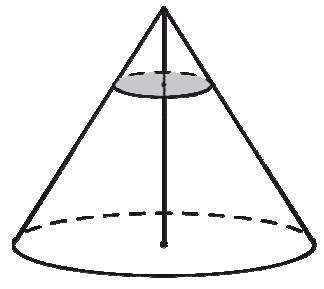 Решение:
Решение:
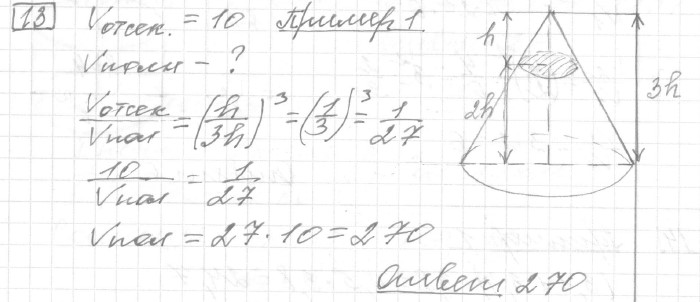 Ответ:
Ответ:
Задание 13 (пример 2)
Текст задачи:Стороны основания правильной треугольной пирамиды равны 16. А боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
 Решение:
Решение:
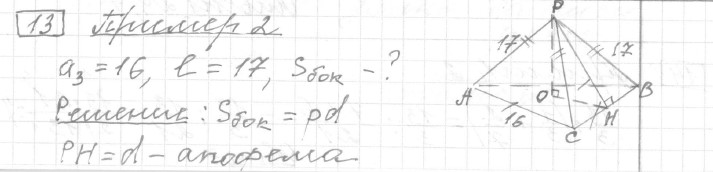
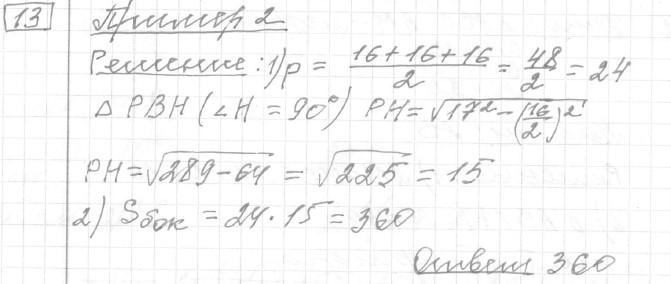 Ответ:
Ответ:
Задание 13 (пример 3)
Текст задачи:Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго — 6 и 4. Во сколько раз объём второго цилиндра больше объёма первого?
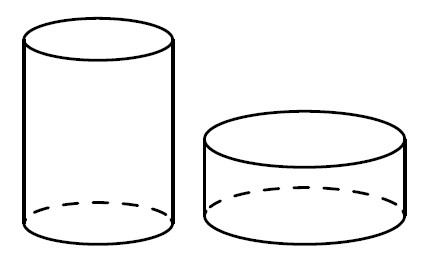 Решение:
Решение:
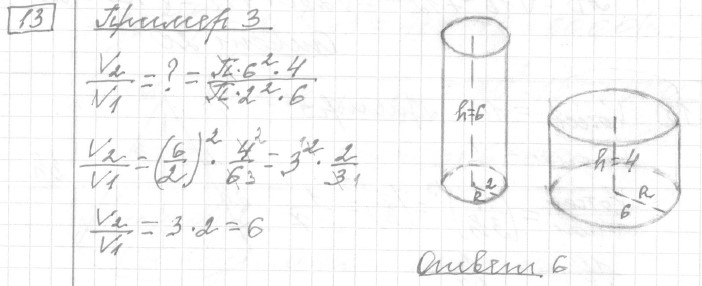 Ответ:
Ответ:
Задание 14 (пример 1)
Текст задачи:Найдите значение выражения .
Решение: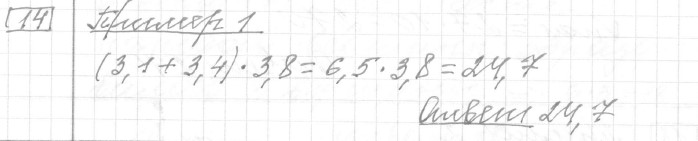 Ответ:
Ответ:
Задание 14 (пример 2)
Текст задачи:Найдите значение выражения
Решение: Ответ:
Ответ:
Задание 15 (пример 1)
Текст задачи:Держатели дисконтной карты книжного магазина получают при покупке скидку 5 %. Книга стоит 280 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
Решение: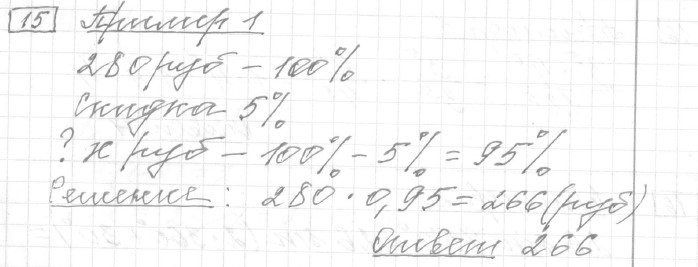 Ответ:
Ответ:
Задание 15 (пример 2)
Текст задачи:Четверть всех отдыхающих в пансионате — дети. Какой процент от всех отдыхающих составляют дети?
Решение: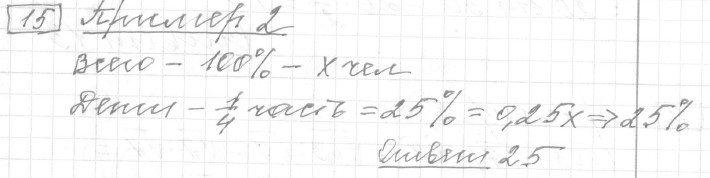 Ответ:
Ответ:
Задание 15 (пример 3)
Текст задачи:Длины двух рек относятся как , при этом одна из них длиннее другой на 10 км. Найдите длину большей реки. Ответ дайте в километрах.
Решение: Ответ:
Ответ:
Задание 16 (пример 1)
Текст задачи:Найдите значение выражения
Решение: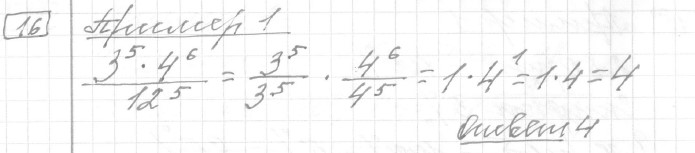 Ответ:
Ответ:
Задание 16 (пример 2)
Текст задачи:Найдите значение выражения .
Решение: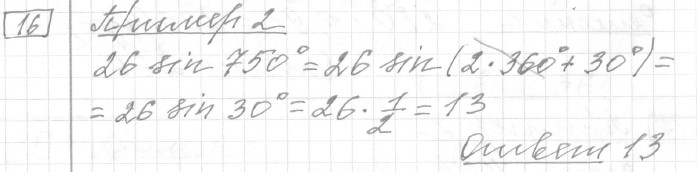 Ответ:
Ответ:
Задание 16 (пример 3)
Текст задачи:Найдите значение выражения
Решение: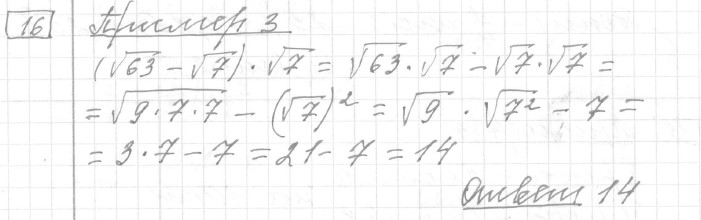 Ответ:
Ответ:
Задание 16 (пример 4)
Текст задачи:Найдите значение выражения
Решение: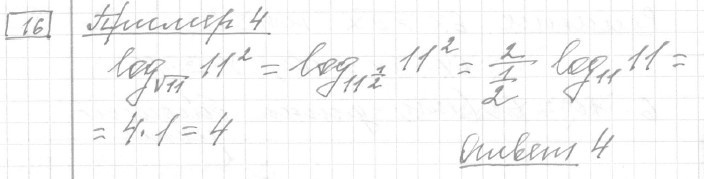 Ответ:
Ответ:
Задание 17 (пример 1)
Текст задачи:Найдите корень уравнения
Решение: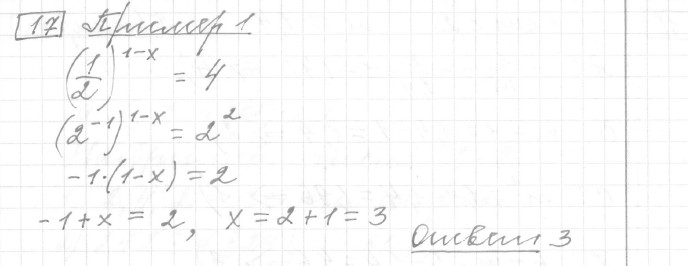 Ответ:
Ответ:
Задание 17 (пример 2)
Текст задачи:Найдите корень уравнения .
Решение: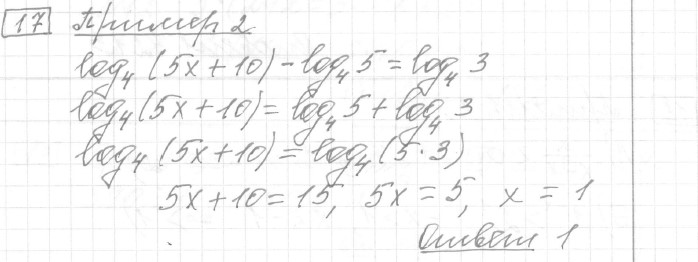 Ответ:
Ответ:
Задание 17 (пример 3)
Текст задачи:Решите уравнение . Если уравнение имеет больше одного корня, в ответе укажите больший из них.
Решение: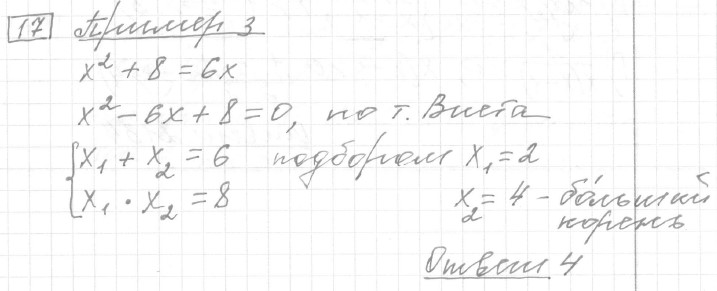 Ответ:
Ответ:
Задание 18 (пример 1)
Текст задачи:На координатной прямой отмечено число m и точки A, B, C и D.

Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИ | ЧИСЛА |
|---|---|
| A | |
| B | |
| C | |
| D |
В таблице под каждой буквой укажите соответствующий номер.
Решение: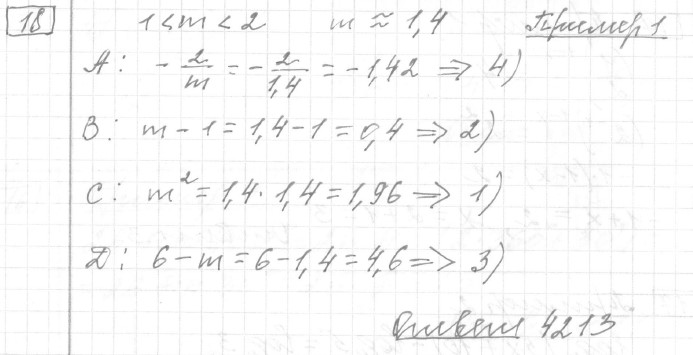 Ответ:
Ответ:
Задание 18 (пример 2)
Текст задачи:Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
|---|---|
| А) | |
| Б) | |
| В) | |
| Г) |
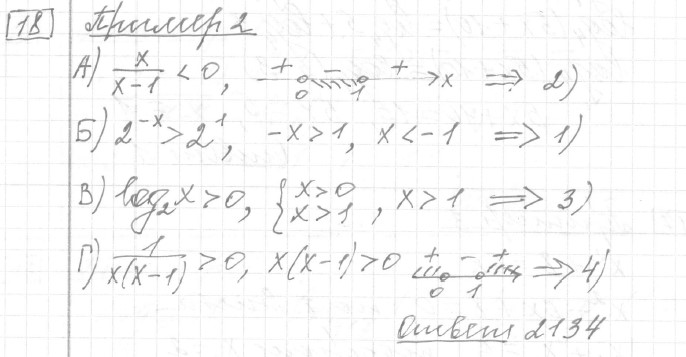 Ответ:
Ответ:
Задание 19 (пример 1)
Текст задачи:Найдите трёхзначное натуральное число, которое при делении и на 4, и на 5, и на 6 даёт в остатке 2 и все цифры в записи которого чётные. В ответе запишите какое-нибудь одно такое число.
Решение: Ответ:
Ответ:
Задание 19 (пример 2)
Текст задачи:На шести карточках написаны цифры 2, 3, 5, 6, 7, 7 (по одной цифре на каждой карточке). В выражении
вместо каждого квадратика положили карточку из этого набора. Оказалось, что полученная сумма делится на 10, но не делится на 20. В ответе укажите какую-либо одну такую сумму.
Решение: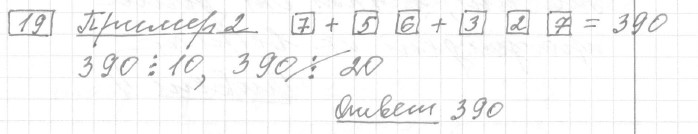 Ответ:
Ответ:
Задание 19 (пример 3)
Текст задачи:Найдите шестизначное натуральное число, которое записывается только цифрами 2 и 0 и делится на 24. В ответе запишите какое-нибудь одно такое число.
Решение: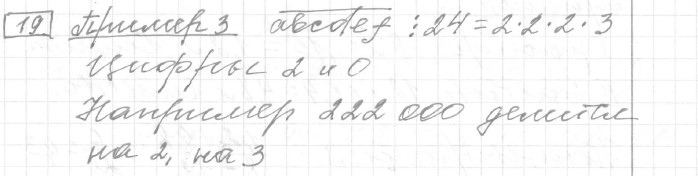 Ответ:
Ответ:
Задание 20 (пример 1)
Текст задачи:Два человека одновременно отправляются из одного дома на прогулку до опушки леса, находящейся в 4,5 км от дома. Один идёт со скоростью 4 км/ч, а другой — со скоростью 5 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от дома произойдёт их встреча? Ответ дайте в километрах.
Решение: Ответ:
Ответ:
Задание 20 (пример 2)
Текст задачи:Смешали 8 литров 15-процентного раствора вещества с 12 литрами 40-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение: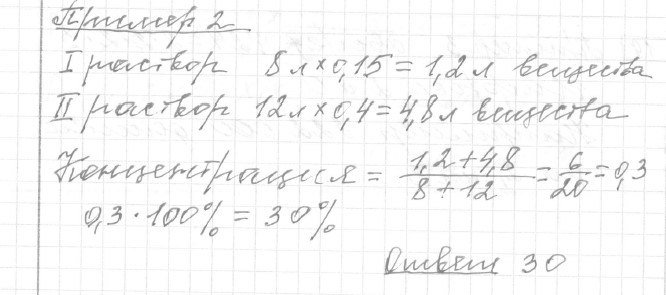 Ответ:
Ответ:
Задание 21 (пример 1)
Текст задачи:Список заданий викторины состоял из 50 вопросов. За каждый правильный ответ ученик получал 9 очков, за неправильный ответ с него списывали 17 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 153 очка, если известно, что по крайней мере один раз он ошибся?
Решение:

 Ответ:
Ответ:
Задание 21 (пример 2)
Текст задачи:Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.
Решение: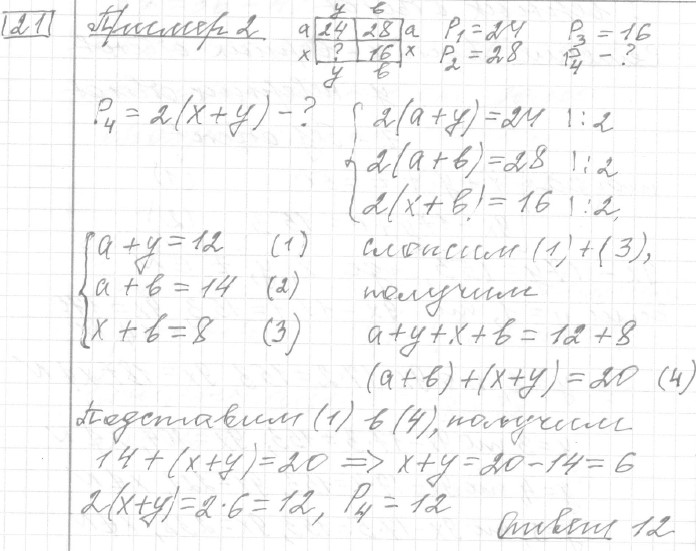 Ответ:
Ответ:
Задание 21 (пример 3)
Текст задачи:На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 9 кусков, если по жёлтым — 7 кусков, а если по зелёным — 6 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
Решение: Ответ:
Ответ:
Задания взяты из демонстрационного варианта для базового уровня ЕГЭ по математике 2025 с сайта ФИПИ https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-2
Файлы для скачивания:





