Задание №1
Пример №1
Баночка йогурта стоит 14 рублей 60 копеек. Какое наибольшее количество баночек йогурта можно купить на 100 рублей?
Решение:
100 : 14.6 = 100 : 14
610 = 100 :
14610 = 100 ×
10146 =
1000146 = 6
124146 ≈ 6 баночек.
Ответ: 6
Пример №2
Килограмм моркови стоит 40 рублей. Олег купил 1 кг 600 г моркови. Сколько рублей сдачи он должен получить со 100 рублей?
Решение:
100 — 40 × 1.6 = 100 — 40 ×
1610 = 100 — 16 × 4 = 100 — 64 = 36 руб.
Ответ: 36
Пример №3
Для ремонта требуется 63 рулона обоев. Какое наименьшее количество пачек обойного клея нужно для такого ремонта, если 1 пачка клея рассчитана на 6 рулонов?
Решение:
63 : 6 = 10.5 пачек ⇒ 11 пачек
Ответ: 11
Задание №2
Пример №1
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| Величины |
Значения |
| А) рост ребёнка |
1) 32 км |
| Б) толщина листа бумаги |
2) 30 м |
| В) протяжённость автобусного маршрута |
3) 0,2 мм |
| Г) высота жилого дома |
4) 110 см |
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Решение:
| Величины |
Значения |
| А) рост ребёнка |
4) 110 см |
| Б) толщина листа бумаги |
3) 0,2 мм |
| В) протяжённость автобусного маршрута |
1) 32 км |
| Г) высота жилого дома |
2) 30 м |
Ответ: 4312
Пример №2
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| Величины |
Значения |
| А) масса взрослого человека |
1) 8 т |
| Б) масса грузового автомобиля |
2) 5 г |
| В) масса книги |
3) 65 кг |
| Г) масса пуговицы |
4) 300 г |
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Решение:
| Величины |
Значения |
| А) масса взрослого человека |
3) 65 кг |
| Б) масса грузового автомобиля |
1) 8 т |
| В) масса книги |
4) 300 г |
| Г) масса пуговицы |
2) 5 г |
Ответ: 3142
Задание №3
Пример №1
На диаграмме приведены данные о длине восьми крупнейших рек России (в тысячах километров). Первое место по длине занимает река Лена.
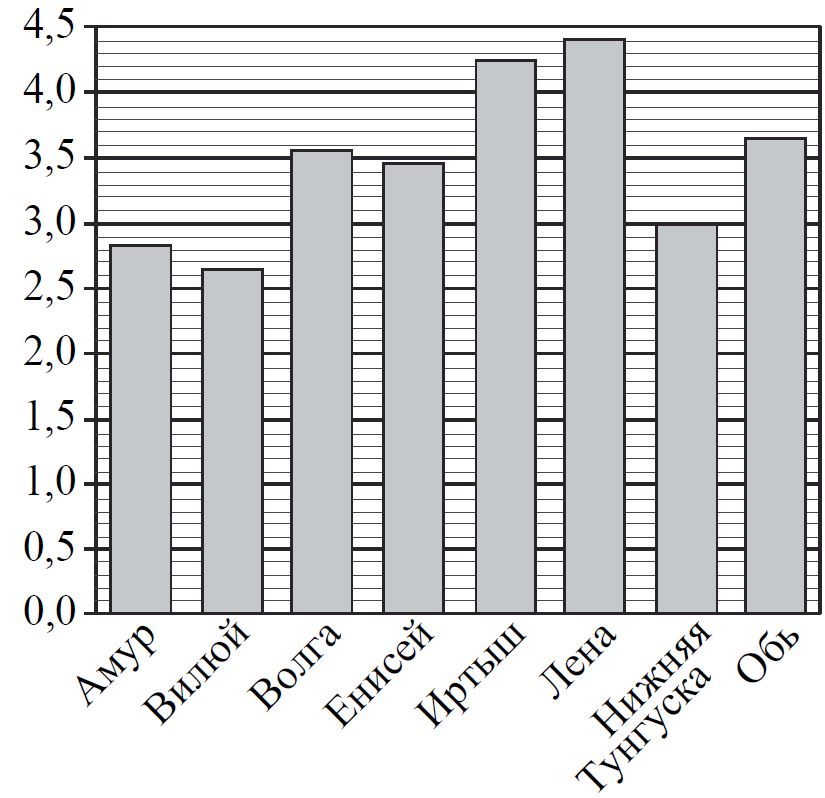
На каком месте по длине находится река Амур?
Решение:
Лена — 1 место
Амур — 7 место
Ответ: 7
Пример №2
В таблице представлены данные о стоимости некоторой модели смартфона в различных магазинах.
| Магазин |
Стоимость смартфона (руб.) |
| «ОК-Техника» |
6733 |
| «Скоростной» |
7600 |
| «Магия связи» |
6559 |
| «Про-фон» |
7346 |
| «Смартфон и Ко» |
6599 |
| «Прогресс-Э» |
7548 |
| «999 телефонов» |
6959 |
| «Макропоиск» |
7049 |
| «Вселенная телефонов» |
6850 |
Найдите наименьшую стоимость смартфона среди представленных предложений. Ответ дайте в рублях.
Решение:
6559 руб — наименьшая стоимость.
Ответ: 6559
Пример №3
На графике показано изменение температуры воздуха на протяжении трёх суток. На горизонтальной оси отмечены число, месяц, время суток в часах; на вертикальной оси – значение температуры в градусах Цельсия.
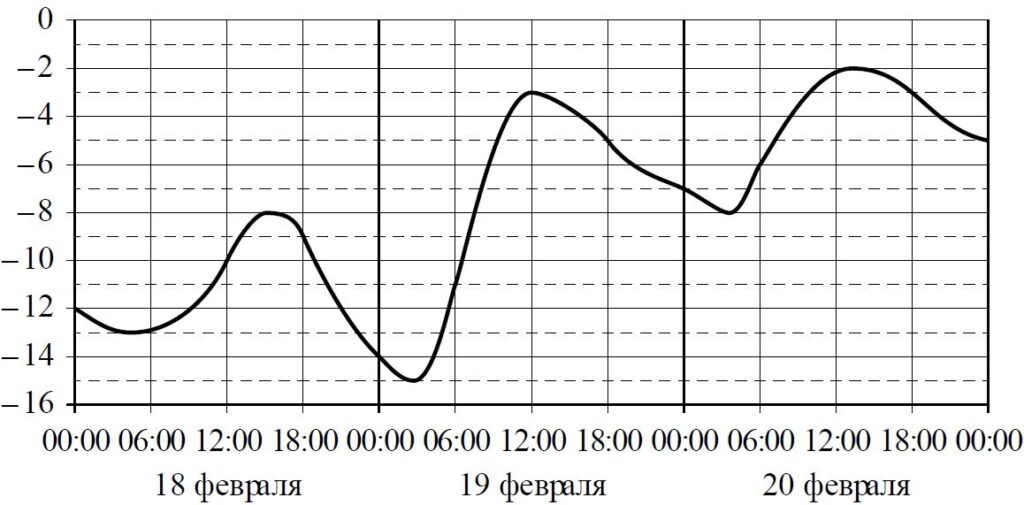
Определите по графику наибольшую температуру воздуха 19 февраля. Ответ дайте в градусах Цельсия.
Решение:
19 февраля -3 ºC наибольшая температура.
Ответ: -3
Задание №4
Пример №1
Мощность постоянного тока (в ваттах) вычисляется по формуле P = I
2R , где I – сила тока (в амперах), R – сопротивление (в омах). Пользуясь этой формулой, найдите P (в ваттах), если R = 5 Ом и I = 7 А.
Решение:
P = 7
2 × 5 = 49 × 5 = 245 Вт.
Ответ: 245
Пример №2
Среднее геометрическое трёх чисел: a, b и c – вычисляется по формуле g = ³√
abc. Вычислите среднее геометрическое чисел 5, 25 и 27.
Решение:
g = ³√
5 × 25 × 27 = ³√
5 × 5² × 3³ = ³√
5³ × 3³ = ³√
(5 × 3)³ = 5 × 3 = 15.
Ответ: 15
Задание №5
Пример №1
В чемпионате по прыжкам в воду участвуют 35 спортсменов: 7 из России, 12 из Китая, 9 из Японии и 7 из США. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из России.
Решение:
P =
77 + 12 + 9 + 7 =
735 =
15 = 0.2
Ответ: 0.2
Пример №2
Из каждых 100 лампочек, поступающих в продажу, в среднем 3 неисправны. Какова вероятность того, что случайно выбранная в магазине лампочка окажется исправной?
Решение:
P =
100 — 3100 =
97100 = 0.97
Ответ: 0.97
Задание №6
Пример №1
Для обслуживания международного семинара необходимо собрать группу переводчиков. Сведения о кандидатах представлены в таблице.
| Номер переводчика |
Язык |
Стоимость услуг (руб. в день) |
| 1 |
Немецкий, испанский |
7000 |
| 2 |
Английский, немецкий |
6000 |
| 3 |
Английский |
3000 |
| 4 |
Английский, французский |
6000 |
| 5 |
Французский |
2000 |
| 6 |
Испанский |
4000 |
Пользуясь таблицей, соберите хотя бы одну группу, в которой переводчики вместе владеют четырьмя иностранными языками: английским, немецким, французским и испанским, а суммарная стоимость их услуг не превышает 12 000 рублей в день.
В ответе укажите какой-нибудь один набор номеров переводчиков (без пробелов, запятых и других дополнительных символов).
Решение:
| Номер переводчика |
Язык |
Стоимость услуг (руб. в день) |
| 1 |
Немецкий, испанский |
7000 |
| 3 |
Английский |
3000 |
| 5 |
Французский |
2000 |
|
|
12000 |
или
| Номер переводчика |
Язык |
Стоимость услуг (руб. в день) |
| 2 |
Английский, немецкий |
6000 |
| 5 |
Французский |
2000 |
| 6 |
Испанский |
4000 |
|
|
12000 |
Ответ: 135
Пример №2
В таблице приведены данные о шести чемоданах.
| Номер чемодана |
Длина (см) |
Высота (см) |
Ширина (см) |
Масса (кг) |
| 1 |
65 |
40 |
25 |
19 |
| 2 |
84 |
72 |
49 |
24 |
| 3 |
92 |
80 |
36 |
23 |
| 4 |
75 |
60 |
45 |
25 |
| 5 |
83 |
65 |
48 |
22,5 |
| 6 |
95 |
75 |
42 |
30 |
По правилам авиакомпании сумма трёх измерений (длина, высота, ширина) чемодана, сдаваемого в багаж, не должна превышать 203 см, а масса не должна быть больше 23 кг. Какие чемоданы можно сдать в багаж по правилам этой авиакомпании?
В ответе укажите номера всех выбранных чемоданов (без пробелов, запятых и других дополнительных символов).
Решение:
Чемоданы под номерами 2, 4, 6 сдать в багаж не получится т.к. они превышают допустимый вес.
Чемоданы под номерами 1, 3, 5 проходят по допустимому весу, посчитаем суммы длин сторон каждого из перечисленных чемоданов.
Чемодан №1 можно сдать в багаж т.к. 65 + 40 + 25 = 130 < 203 Чемодан №3 нельзя сдать в багаж т.к. 92 + 80 + 36 = 208 > 203
Чемодан №5 можно сдать в багаж т.к. 83 + 65 + 48 = 196 < 203
Ответ: 15
Пример №3
Строительная фирма планирует купить 70 м
3 пеноблоков у одного из трёх поставщиков. Цены и условия доставки приведены в таблице.
| Поставщик |
Стоимость пеноблоков (руб. за 1 м3) |
Стоимость доставки (руб.) |
Дополнительные условия |
| А |
2600 |
10000 |
Нет |
| Б |
2800 |
8000 |
При заказе товара на сумму свыше 150000 рублей доставка бесплатная |
| В |
2700 |
8000 |
При заказе товара на сумму свыше 200000 рублей доставка бесплатная |
Сколько рублей нужно заплатить за самую дешёвую покупку с доставкой?
Решение:
Поставщик А: 70 × 2600 + 10000 = 192000 руб.
Поставщик Б: 70 × 2800 = 196000 руб. т.к. сумма заказа больше 150000 руб. доставка будет бесплатная.
Поставщик В: 70 × 2700 + 8000 = 197000 руб.
Ответ: 192000
Задание №7
Пример №1
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
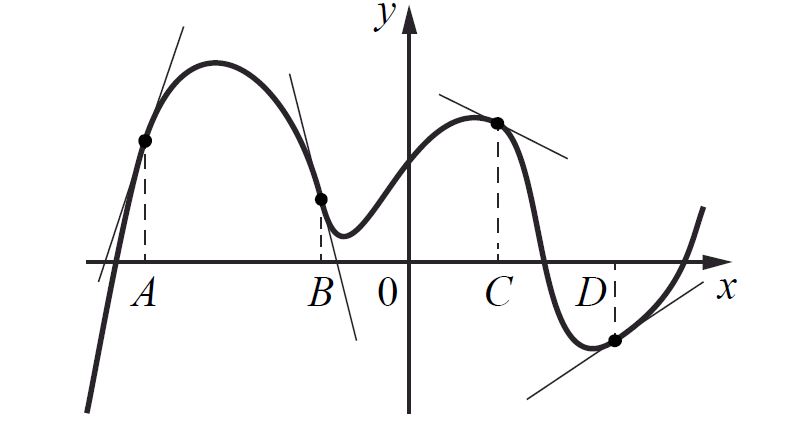
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
| Точки |
Значения производной |
| A |
-4 |
| B |
3 |
| C |
23 |
| D |
-0.5 |
В таблице под каждой буквой укажите соответствующий номер.
Решение:
A: α
A — острый угол ⇒ ƒ’(X
A) = 3 → 2
B: α
B — тупой угол ⇒ ƒ’(X
B) = -4 → 1
C: α
C — тупой угол ⇒ ƒ’(X
C) = -0.5 → 4
D: α
D — острый угол ⇒ ƒ’(X
D) =
23 → 3
Ответ: 2143
Пример №2
На графике изображена зависимость температуры от времени в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя; на вертикальной оси – температура двигателя в градусах Цельсия.
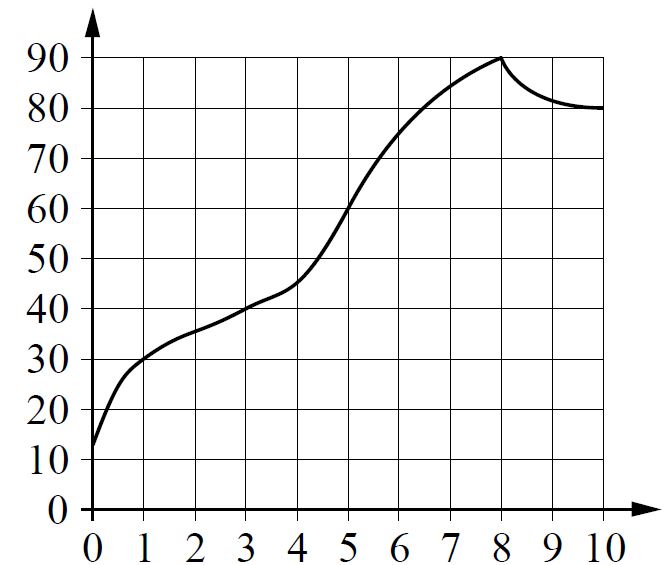
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.
| Интервалы времени |
Характеристики |
| А) 0–1 мин. |
1) Рост температуры был самым медленным |
| Б) 1–3 мин. |
2) Температура падала |
| В) 3–6 мин. |
3) Температура находилась в пределах от 40 °C до 80 °C |
| Г) 8–10 мин. |
4) Температура не превышала 30 °C |
В таблице под каждой буквой укажите соответствующий номер.
Решение:
А → 4
Б → 1
В → 3
Г → 2
Ответ: 4132
Пример №3
Установите соответствие между графиками функций и характеристиками этих функций на отрезке [−1; 1].
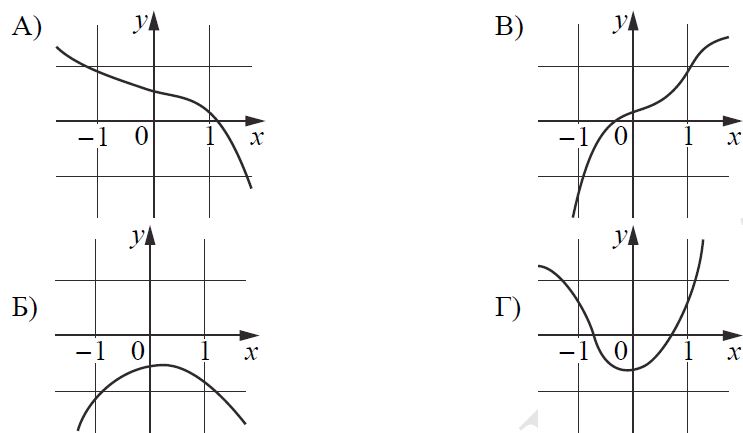
Характеристики
1) Функция имеет точку максимума на отрезке [−1; 1].
2) Функция имеет точку минимума на отрезке [−1; 1].
3) Функция возрастает на отрезке [−1; 1].
4) Функция убывает на отрезке [−1; 1].
В таблице под каждой буквой укажите соответствующий номер.
Решение:
А → 4
Б → 1
В → 3
Г → 2
Ответ: 4132
Задание №8
Пример №1
В классе учится 20 человек, из них 13 человек посещают кружок по истории, а 10 – кружок по математике. Выберите утверждения, которые верны при указанных условиях.
1) Каждый ученик этого класса посещает оба кружка.
2) Найдётся хотя бы двое учеников из этого класса, посещающих оба кружка.
3) Если ученик из этого класса ходит на кружок по истории, то он обязательно ходит на кружок по математике.
4) Не найдётся 11 человек из этого класса, которые посещают оба кружка.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Решение:
История — 13 человек
Математика — 10 человек
Всего — 20 человек
| Утверждение |
Верность утверждения |
| 1) Каждый ученик этого класса посещает оба кружка. |
ложь |
| 2) Найдётся хотя бы двое учеников из этого класса, посещающих оба кружка. |
истина |
| 3) Если ученик из этого класса ходит на кружок по истории, то он обязательно ходит на кружок по математике. |
ложь |
| 4) Не найдётся 11 человек из этого класса, которые посещают оба кружка. |
истина |
Ответ: 24
Пример №2
Во дворе школы растут всего три дерева: ясень, рябина и осина. Ясень выше рябины на 1 метр, но ниже осины на 2 метра. Выберите все утверждения, которые верны при указанных условиях.
1) Среди указанных деревьев не найдётся двух одной высоты.
2) Ясень, растущий во дворе школы, выше осины, растущей там же.
3) Любое дерево помимо указанных, которое ниже ясеня, растущего во дворе школы, также ниже рябины, растущей там же.
4) Любое дерево помимо указанных, которое ниже рябины, растущей во дворе школы, также ниже ясеня, растущего там же.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Решение:

| Утверждение |
Верность утверждения |
| 1) Среди указанных деревьев не найдётся двух одной высоты. |
истина |
| 2) Ясень, растущий во дворе школы, выше осины, растущей там же. |
ложь |
| 3) Любое дерево помимо указанных, которое ниже ясеня, растущего во дворе школы, также ниже рябины, растущей там же. |
ложь |
| 4) Любое дерево помимо указанных, которое ниже рябины, растущей во дворе школы, также ниже ясеня, растущего там же. |
истина |
Ответ: 14
Задание №9
Пример №1
На рисунке изображён план местности (шаг сетки плана соответствует расстоянию 1 км на местности). Оцените, скольким квадратным километрам равна площадь озера Великое, изображённого на плане. Ответ округлите до целого числа.
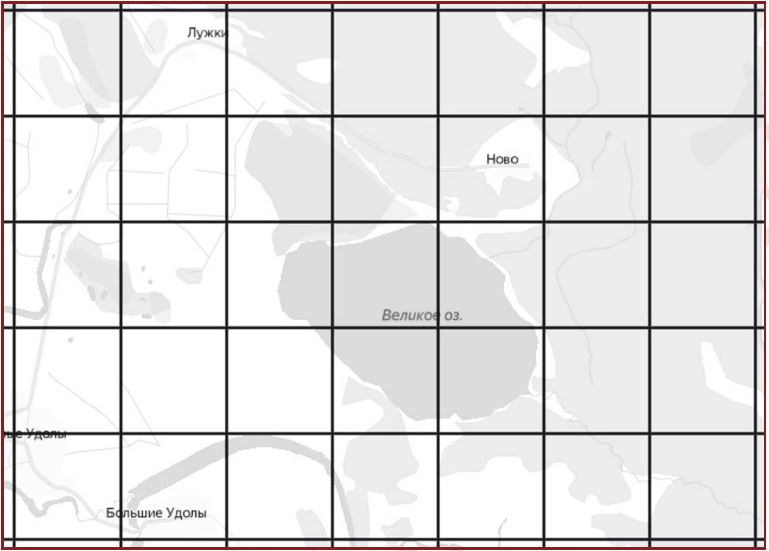 Решение:
Решение:
S
озера ≈ 3 км
2
Ответ: 3
Пример №2
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане.
Ответ дайте в квадратных метрах.
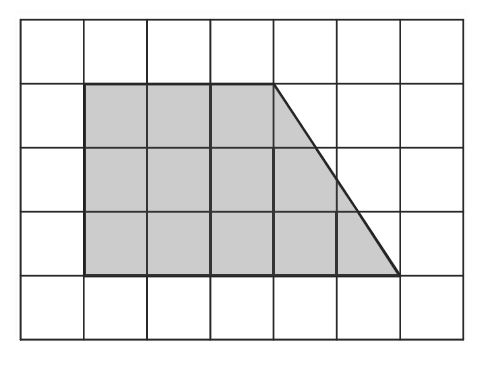 Решение:
Решение:
S
трапеции =
3 + 52 × 3 = 12 м
2
Ответ: 12
Задание №10
Пример №1
Дачный участок имеет форму прямоугольника со сторонами 25 метров и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите суммарную длину забора в метрах.
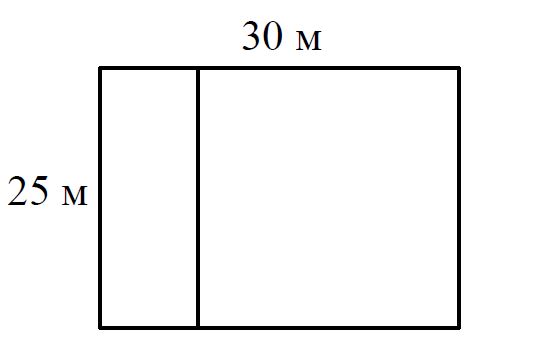 Решение:
Решение:
Длина забора равна периметру прямоугольника плюс 25 м.
Длина забора = 2 × (30 + 25) + 25 = 135 м.
Ответ: 135
Пример №2
Какой угол (в градусах) образуют минутная и часовая стрелки в 16:00?
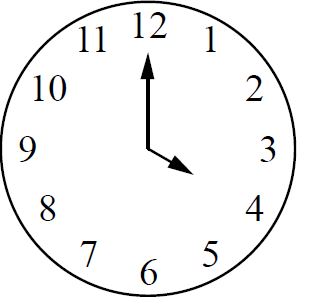 Решение:
Решение:
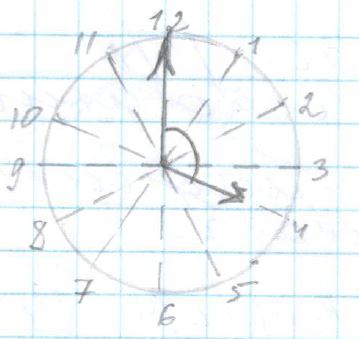
360
o : 12 × 4 = 120
o
Ответ: 120
Задание №11
Пример №1
Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у данного? Ответ дайте в сантиметрах.
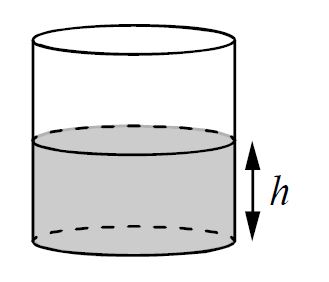 Решение:
Решение:
|
Было |
Стало |
| Высота |
80 |
h? |
| Радиус |
R |
4R |
| Объем |
πR2×80 |
π(4R)2h |
80πR
2 = π16R
2h
80 = 16h
h = 5
Ответ: 5
Пример №2
От деревянного кубика отпилили все его вершины (см. рисунок). Сколько граней у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
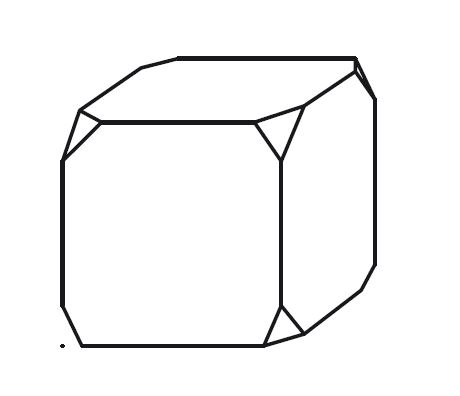 Решение:
Решение:
На месте каждой из 8 вершин куба образовалась одна грань.
Было 6 граней, стало 6 + 8 = 14 граней
Ответ: 14
Задание №12
Известно, что в треугольнике ABC AB = BC = 13, AC = 10 . Найдите длину медианы BM.
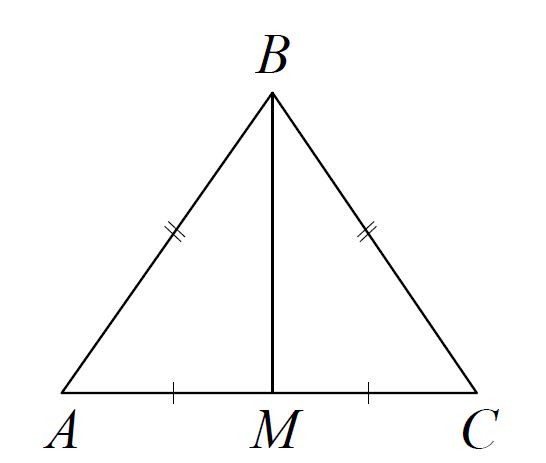 Решение:
Решение:
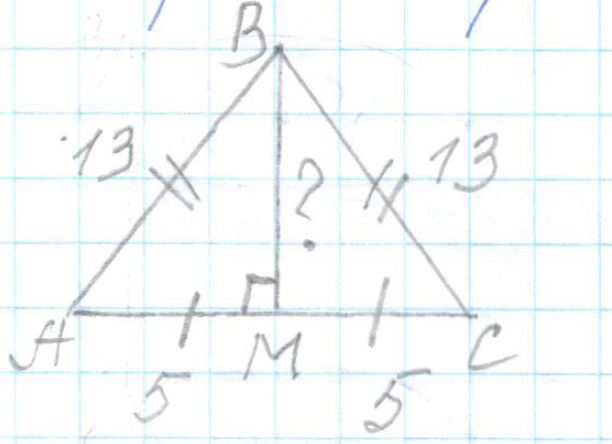
1) Δ ABC — равнобедренный треугольник. АС — основание
2) BM — медиана ⇒ высота
3) Δ ABM (∠M = 90
o)
BM = √
13² — 5² = √
169 — 25 = √
144 = 12
Ответ: 12
Задание №13
Пример №1
Радиус основания цилиндра равен 13, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.
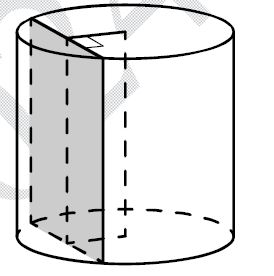 Решение:
Решение:
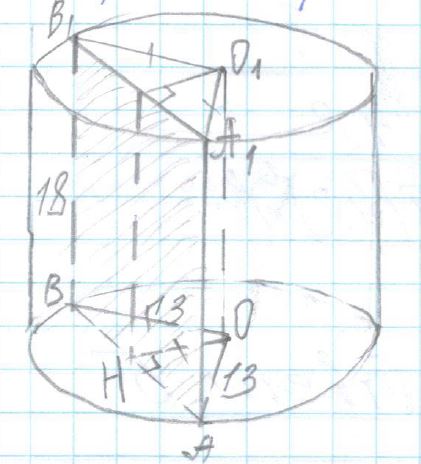
R = 13 L = 18 h = 12 = OH
S
сечения = ? = S
ABB1A1 = 18AB
1) Δ AOB — равнобедренный с основанием AB
OH AB ⇒ OH — медиана
AH = HB =
12AB
2) Δ AOH (∠ H = 90
o) по теореме Пифагора AH = √
13² — 12² = 5
3) AB = 2AH = 2 × 5 = 10
4) S
сечения = 18 × 10 = 180
Ответ: 180
Пример №2
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно √
17.
 Решение:
Решение:
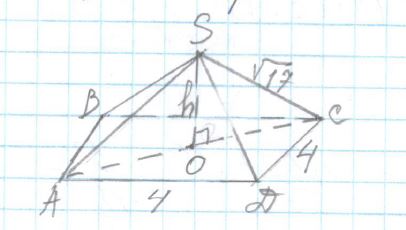
SABCD — правильная четырехугольная пирамида ⇒ ABCD — квадрат
a = 4
L = √
17
V
SABCD = ?
V
пирамида =
13 S
ABCD × h =
13 × 4
2 × h =
163h
1) AC = a√
2 = 4√
2
OC =
12AC =
12 × 4√
2 = 2√
2
2) Δ SOC (∠O = 90
o)
SO = √
(√17)² — (2√2)² = √
17 — 8 = √
9 = 3
3) V
пирамиды =
163 × 3 = 16
Ответ: 16
Пример №3
Даны два шара радиусами 9 и 3. Во сколько раз площадь поверхности большего шара больше площади поверхности меньшего?
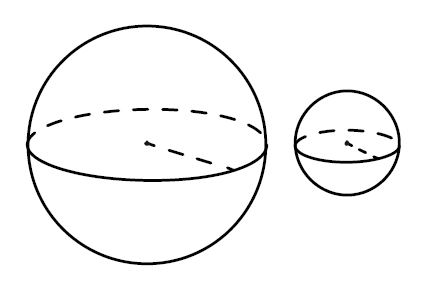 Решение:
4πR124πR22
Решение:
4πR124πR22 = (
93)
2 = 3
2 = 9
Ответ: 9
Задание №14
Пример №1
Найдите значение выражения (6,7 − 3,2)⋅ 2,4
Решение:
(6.7 — 3.2) × 2.4 = 3.5 × 2.4 = 8.4
Ответ: 8.4
Пример №2
Найдите значение выражения (
833 +
1322) :
518
Решение:
(
833 +
1322) :
518 =
16 + 3966 :
518 =
55 × 1866 × 5 = 3
Ответ: 3
Задание №15
Пример №1
Ивану Кузьмичу начислена заработная плата 20000 рублей. Из этой суммы вычитается налог на доходы физических лиц в размере 13 %. Сколько рублей Иван Кузьмич получит после уплаты этого налога?
Решение:
20000 руб × (1 — 0.13) = 20000 × 0.87 = 17400 руб
Ответ: 17400
Пример №2
ЕГЭ по физике сдавали 25 выпускников школы, что составляет треть от общего числа выпускников. Сколько выпускников этой школы не сдавали экзамена по физике?
Решение:
1) 25 :
13 = 25 × 3 = 75 человек всего
2) 75 — 25 = 50 человек не сдавали физику
Ответ: 50
Пример №3
Площадь земель фермерского хозяйства, отведённых под посадку сельскохозяйственных культур, составляет 24 гектара и распределена между зерновыми и овощными культурами в отношении 5 : 3 соответственно.
Сколько гектаров занимают овощные культуры?
Решение:
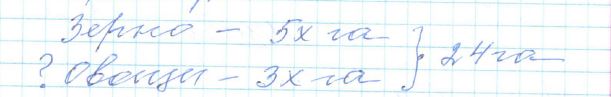
5x + 3x = 24
8x = 24
x = 3
3x = 3 × 3 = 9 (га) овощи
Ответ: 9
Задание №16
Пример №1
Найдите значение выражения
14927 × 78
Решение:
14927 × 78 =
29 × 7927 × 78 = 2
9 — 7 × 7
9 — 8 = 2
2 × 7
1 = 4 × 7 = 28
Ответ: 28
Пример №2
Найдите cosα , если sinα = 0,8 и 90° < α < 180°.
Решение:
cosα = — √
1 — 0.8²
α ∈ II четверть, где cosα < 0
cosα = -√
1 — 0.64
cosα = -√
0.36
cosα = -0.6
Ответ: -0.6
Пример №3
Найдите значение выражения (2√
13 — 1)(2√
13 + 1).
Решение:
(2√
13 — 1)(2√
13 + 1) = (2√
13)
2 — 1
2 = 4 × 13 — 1 = 52 — 1 = 51
Ответ: 51
Пример №4
Найдите значение выражения log
31.8 + log
35.
Решение:
log
31.8 + log
35 = log
3(1.8 × 5) = log
39 = 2
Ответ: 2
Задание №17
Пример №1
Найдите корень уравнения 3
x — 3 = 81.
Решение:
3
x — 3 = 81
3
x — 3 = 3
4
x — 3 = 4
x = 7
Ответ: 7
Пример №2
Найдите корень уравнения log
2(x − 3) = 6.
Решение:
log
2(x − 3) = 6
x — 3 = 2
6
x — 3 = 64
x = 64 + 3
x = 67
Ответ: 67
Пример №3
Решите уравнение x
2 − x − 6 = 0.
Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Решение:
x
2 − x − 6 = 0
x
1 = -2
x
2 = 3
по теореме Виета

x
1 + x
2 = 1 = -b
x
1 × x
2 = -6 = c

-2 + 3 = 1
-2 × 3 = -6
-2 меньший корень
Ответ: -2
Задание №18
Пример №1
На координатной прямой отмечены точки A, B, C и D.
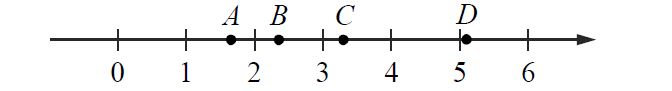
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| Точки |
Числа |
| A |
log210 |
| B |
73 |
| C |
√26 |
| D |
(35)-1 |
Решение:
1) log
210 ≈ 3.3 ⇒ C
2)
73 = 2
13 ⇒ B
3) √
26 ≈ 5.1 ⇒ D
4) (
35)
-1 =
53 = 1
23 ⇒ A
Ответ: 4213
Пример №2
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| Неравенства |
Решения |
| 2x ≥ 4 |
 |
| 0.5x ≥ 4 |
 |
| 0.5x ≤ 4 |
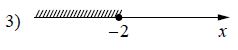 |
| 2x ≤ 4 |
 |
В таблице под каждой буквой укажите соответствующий номер.
Решение:
А) 2
x ≥ 4
2
x ≥ 2
2
x ≥ 2 ⇒ 4
Б) 0.5
x ≥ 4
0.5
x ≥ 0.5
-2
x ≤ -2 ⇒ 3
В) 0.5
x ≤ 4
0.5
x ≤ 0.5
-2
x ≥ -2 ⇒ 2
Г) 2
x ≤ 4
2
x ≤ 2
2
x ≤ 2 ⇒ 1
Ответ: 4321
Задание №19
Пример №1
Найдите трёхзначное число, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9. В ответе укажите какое-либо одно такое число.
Решение:
5 + 7 + 8 = 20
5
2 + 7
2 + 8
2 = 25 + 49 + 64 = 138
138 делится на 3 без остатка, но не делится на 9 без остатка.
Ответ: 578
Пример №2
На шести карточках написаны цифры 2, 3, 5, 6, 7, 7 (по одной цифре на каждой карточке). В выражении
□ + □ □ + □ □ □
вместо каждого квадратика положили карточку из данного набора. Оказалось, что полученная сумма делится на 10, но не делится на 20. В ответе укажите какую-либо одну такую сумму.
Решение:
7 + 27 + 356 = 390
390 делится без остатка на 10, но не делится без остатка на 20
Ответ: 390
Пример №3
Вычеркните в числе 75157613 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое-либо одно получившееся число.
Решение:
751576
13
51576 ⋮ 12 — делится без остатка
Ответ: 51576
Задание №20
Пример №1
Расстояние между городами А и В равно 470 км. Из города А в город В выехал первый автомобиль, а через 3 часа после этого навстречу ему из города В выехал со скоростью 60 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города А. Ответ дайте в км/ч.
Решение:
1) S
2 = 470 км — 350 км = 120 км
2) t
2 = 120 км : 60 км/ч = 2ч
3) t
1 = 2 ч + 3 ч = 5 ч
4) V
1 = 70 км/ч
Ответ: 70
Пример №2
В понедельник акции компании подорожали на некоторое число процентов, а во вторник подешевели на то же самое число процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Решение:
p — процент
|
Было |
Стало |
| Пн |
x |
(1 + 0.01p)x |
| Вт |
(1 + 0.01p)x |
(1 + 0.01p)x — 0.01p(1 + 0.01p)x |
x — (1 + 0.01p)(1 — 0.01p)xx = 0.04
1 — (1 + 0.01p)(1 — 0.01p) = 0.04
1 — 1 + 0.0001p
2 = 0.04
p
2 = 400
p = 20%
Ответ: 20
Задание №21
Пример №1
Маша и Медведь съели 160 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь – печенье, но в какой-то момент они поменялись. Медведь и то и другое ест в 3 раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?
Решение:
1) Известно, что Маша и Медведь съели варенья поровну, значит, Маша ела варенье в три раза больше времени, чем варенье ел Медведь ⇒ Медведь по времени ел печенье в три раза больше чем печенье ела Маша.
2) Медведь ел печенье в 3 раза быстрее Маши. Значит, на 1 съеденное Машей печенье приходится 3 съеденных печенья Медведем.
3) Если Маша съела x — печений, тогда Медведь съел 3 × 3x = 9x печений.
4) Известно, что Маша и Медведь съели 160 печений вместе ⇒ x + 9x = 160 ⇒ x = 16 печений съела Маша
5) 9 × 16 = 144 печений съел Медведь
Ответ: 144
Пример №2
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.
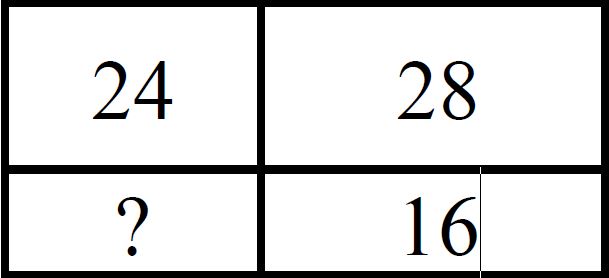 Решение:
Решение:
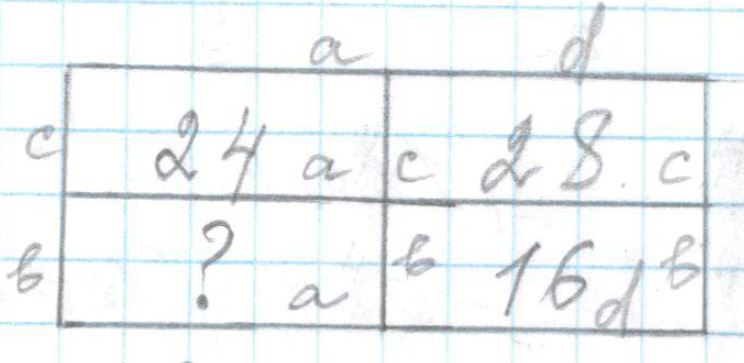
⎧ P
1 = 24 = 2(a + c)
⎨ P2 = 28 = 2(c + d)
⎩ P3 = 16 = 2(b + d)
P4 = ? = 2(a + b)
24 + 28 + 16 = 2(a + c + c + d + b + d)
68 = 2((a + b) + 2(c + d))
34 = (a + b) + 28
a + b = 34 — 28
a + b = 6
P4 = 2 × 6 = 12
Ответ: 12
Пример №3
В доме всего 14 квартир с номерами от 1 до 14. В каждой квартире живёт не менее 1 и не более 4 человек. В квартирах с 1-й по 12-ю включительно живёт суммарно 14 человек, а в квартирах с 11-й по 14-ю включительно живёт суммарно 12 человек. Сколько всего человек живут в этом доме?
Решение:
Расселим жильцов по квартирам:
с 1
ой по 10
ую — по 1 человеку
в 11
ой и 12
ой — по 2 человека
в 13
ой и 14
ой — по 4 человека
Всего: 10 + 2 × 2 + 2 × 4 = 10 + 4 + 8 = 22 человека
Ответ: 22
Задания взяты из демонстрационного варианта для базового уровня ЕГЭ по математике 2024 с сайта ФИПИ https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-2
Файлы для скачивания:
- Демонстрационный вариант для базового уровня Скачать
- Спецификация для базового уровня Скачать
- Кодификатор Скачать
 На каком месте по длине находится река Амур?
Решение:
Лена — 1 место
Амур — 7 место
Ответ: 7
На каком месте по длине находится река Амур?
Решение:
Лена — 1 место
Амур — 7 место
Ответ: 7
 Определите по графику наибольшую температуру воздуха 19 февраля. Ответ дайте в градусах Цельсия.
Решение:
19 февраля -3 ºC наибольшая температура.
Ответ: -3
Определите по графику наибольшую температуру воздуха 19 февраля. Ответ дайте в градусах Цельсия.
Решение:
19 февраля -3 ºC наибольшая температура.
Ответ: -3
 В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
 Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.
 Характеристики
1) Функция имеет точку максимума на отрезке [−1; 1].
2) Функция имеет точку минимума на отрезке [−1; 1].
3) Функция возрастает на отрезке [−1; 1].
4) Функция убывает на отрезке [−1; 1].
В таблице под каждой буквой укажите соответствующий номер.
Решение:
А → 4
Б → 1
В → 3
Г → 2
Ответ: 4132
Характеристики
1) Функция имеет точку максимума на отрезке [−1; 1].
2) Функция имеет точку минимума на отрезке [−1; 1].
3) Функция возрастает на отрезке [−1; 1].
4) Функция убывает на отрезке [−1; 1].
В таблице под каждой буквой укажите соответствующий номер.
Решение:
А → 4
Б → 1
В → 3
Г → 2
Ответ: 4132
 Решение:
S озера ≈ 3 км2
Ответ: 3
Решение:
S озера ≈ 3 км2
Ответ: 3
 Решение:
S трапеции = 3 + 52 × 3 = 12 м2
Ответ: 12
Решение:
S трапеции = 3 + 52 × 3 = 12 м2
Ответ: 12
 Решение:
Длина забора равна периметру прямоугольника плюс 25 м.
Длина забора = 2 × (30 + 25) + 25 = 135 м.
Ответ: 135
Решение:
Длина забора равна периметру прямоугольника плюс 25 м.
Длина забора = 2 × (30 + 25) + 25 = 135 м.
Ответ: 135
 Решение:
Решение:
 360o : 12 × 4 = 120o
Ответ: 120
360o : 12 × 4 = 120o
Ответ: 120
 Решение:
Решение:
 Решение:
На месте каждой из 8 вершин куба образовалась одна грань.
Было 6 граней, стало 6 + 8 = 14 граней
Ответ: 14
Решение:
На месте каждой из 8 вершин куба образовалась одна грань.
Было 6 граней, стало 6 + 8 = 14 граней
Ответ: 14
 Решение:
Решение:
 1) Δ ABC — равнобедренный треугольник. АС — основание
2) BM — медиана ⇒ высота
3) Δ ABM (∠M = 90o)
BM = √13² — 5² = √169 — 25 = √144 = 12
Ответ: 12
1) Δ ABC — равнобедренный треугольник. АС — основание
2) BM — медиана ⇒ высота
3) Δ ABM (∠M = 90o)
BM = √13² — 5² = √169 — 25 = √144 = 12
Ответ: 12
 Решение:
Решение:
 R = 13 L = 18 h = 12 = OH
Sсечения = ? = SABB1A1 = 18AB
1) Δ AOB — равнобедренный с основанием AB
OH AB ⇒ OH — медиана
AH = HB = 12AB
2) Δ AOH (∠ H = 90o) по теореме Пифагора AH = √13² — 12² = 5
3) AB = 2AH = 2 × 5 = 10
4) S сечения = 18 × 10 = 180
Ответ: 180
R = 13 L = 18 h = 12 = OH
Sсечения = ? = SABB1A1 = 18AB
1) Δ AOB — равнобедренный с основанием AB
OH AB ⇒ OH — медиана
AH = HB = 12AB
2) Δ AOH (∠ H = 90o) по теореме Пифагора AH = √13² — 12² = 5
3) AB = 2AH = 2 × 5 = 10
4) S сечения = 18 × 10 = 180
Ответ: 180
 Решение:
Решение:
 SABCD — правильная четырехугольная пирамида ⇒ ABCD — квадрат
a = 4
L = √17
V SABCD = ?
V пирамида = 13 S ABCD × h = 13 × 42 × h = 163h
1) AC = a√2 = 4√2
OC = 12AC = 12 × 4√2 = 2√2
2) Δ SOC (∠O = 90o)
SO = √(√17)² — (2√2)² = √17 — 8 = √9 = 3
3) V пирамиды = 163 × 3 = 16
Ответ: 16
SABCD — правильная четырехугольная пирамида ⇒ ABCD — квадрат
a = 4
L = √17
V SABCD = ?
V пирамида = 13 S ABCD × h = 13 × 42 × h = 163h
1) AC = a√2 = 4√2
OC = 12AC = 12 × 4√2 = 2√2
2) Δ SOC (∠O = 90o)
SO = √(√17)² — (2√2)² = √17 — 8 = √9 = 3
3) V пирамиды = 163 × 3 = 16
Ответ: 16
 Решение:
4πR124πR22 = (93)2 = 32 = 9
Ответ: 9
Решение:
4πR124πR22 = (93)2 = 32 = 9
Ответ: 9
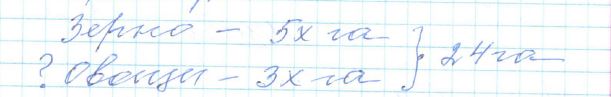 5x + 3x = 24
8x = 24
x = 3
3x = 3 × 3 = 9 (га) овощи
Ответ: 9
5x + 3x = 24
8x = 24
x = 3
3x = 3 × 3 = 9 (га) овощи
Ответ: 9
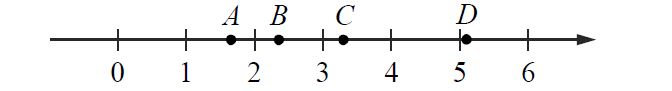 Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.

 Решение:
Решение:
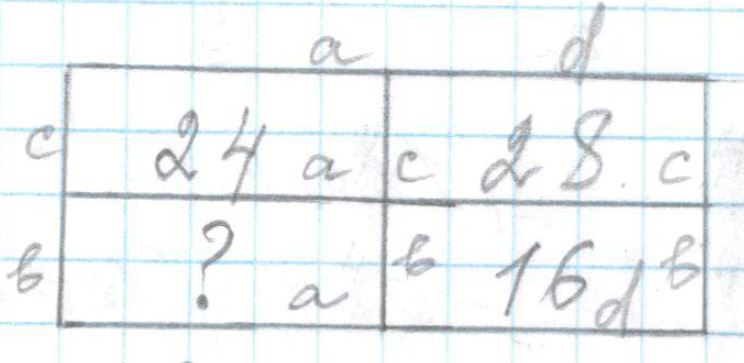 ⎧ P1 = 24 = 2(a + c)
⎧ P1 = 24 = 2(a + c)





