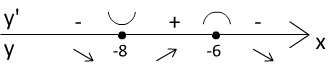Часть 1
Задание 1 (пример 1)
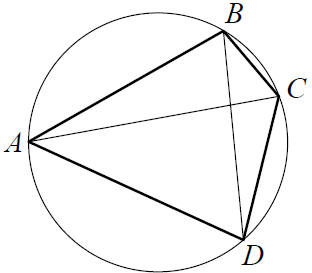
Текст задачи:Четырёхугольник ABCD вписан в окружность. Угол ABC равен 103°, угол CAD равен 42°. Найдите угол ABD. Ответ дайте в градусах.
 Дано:
Дано:
- ABCD вписан в окружность;
- ∠ABC = 103°;
- ∠CAD = 42°
∠ABD
Решение: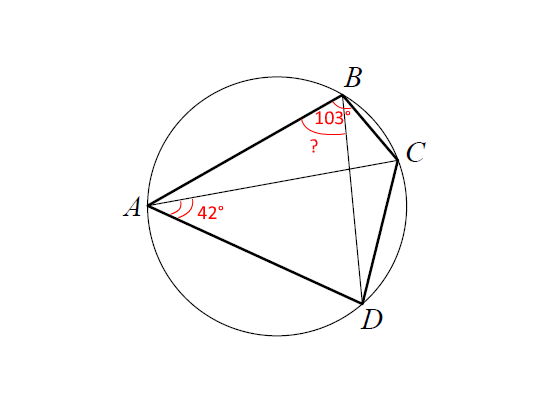
- ∠CAD = ∠CBD = 42° т.к. вписанные углы, опирающиеся на одну и ту же дугу CD, равны.
- ∠ABD = 103° − 42° = 61°
Задание 1 (пример 2)
Текст задачи:Площадь параллелограмма ABCD равна 24. Точка E — середина стороны AD. Найдите площадь трапеции BCDE.
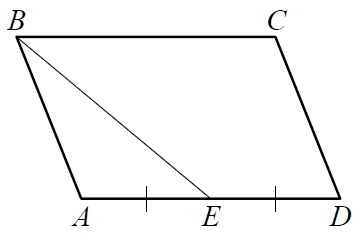 Дано:
Дано:
- ABCD параллелограмм;
- ;
- E — середина AD.
- BD — медиана треугольника ABD
Задание 1 (пример 3)
Текст задачи:В треугольнике ABC стороны AC и ВC равны, угол C равен 134° , угол CBD — внешний. Найдите угол CBD . Ответ дайте в градусах.
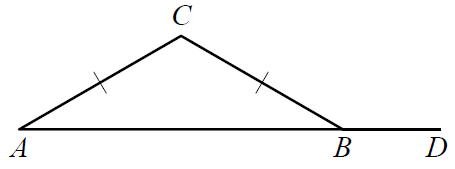 Дано:
Дано:
- ΔABC, AC = BC
- ∠C = 134°
- ∠CBD — внешний
∠CBD
Решение:- ΔABC — равнобедренный ⇒ ∠A = ∠B = (180° − 134°) : 2 = 23°
- ∠CBD = 180° − 23° = 157° (свойство смежных углов)
Задание 1 (пример 4)
Текст задачи:Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
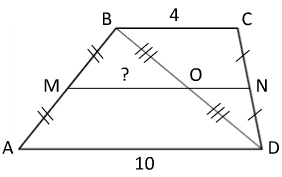 Дано:
Дано:
- ABCD — трапеция;
- AD = 10;
- BC = 4;
- MN — средняя линия;
- BD — диагональ.
MO
Решение:- AD > BC ⇒ MO > NO
- MO — средняя линия треугольника ABD ⇒
Задание 2 (пример 1)
Текст задачи:На координатной плоскости изображены векторы и . Найдите скалярное произведение
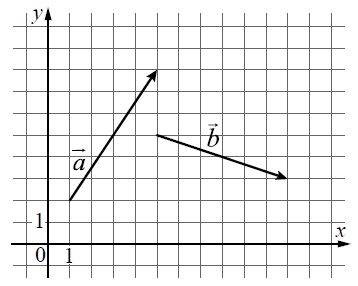 Дано:
Дано:
,
Найти: Решение:- Пусть
и
, тогда
Задание 2 (пример 2)
Текст задачи:Даны векторы и . Найдите длину вектора .
Дано:Длину
Решение:Задание 3 (пример 1)
Текст задачи:Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объёма второй кружки к объёму первой.
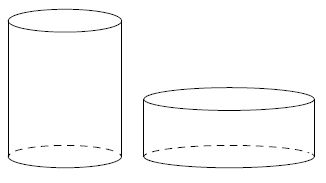 Дано:
Дано:
- Цилиндр 1: R, 2h
- Цилиндр 2: 1.5R, h
Ответ: 1.125
Задание 3 (пример 2)
Текст задачи:Стороны основания правильной четырёхугольной пирамиды равны 10, боковые рёбра равны 13. Найдите площадь поверхности этой пирамиды.
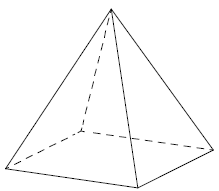 Дано:
Дано:
- — правильная пирамида;
- ,
где полупериметр основания,
d — апофема (высота боковой грани).
- по теореме Пифагора
Задание 3 (пример 3)
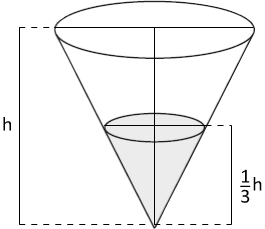
Текст задачи:В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём жидкости равен 4 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
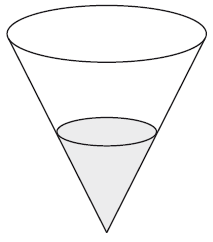 Дано:
Дано:
- конус, h — высота;
- — высота жидкости;
Задание 4 (пример 1)
Текст задачи:В группе туристов 20 человек. С помощью жребия они выбирают семь человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт в магазин?
Решение: Ответ: 0.35Задание 4 (пример 2)
Текст задачи:Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19 включительно.
Решение: Ответ: 0.38Задание 5 (пример 1)
Текст задачи:Помещение освещается тремя лампами. Вероятность перегорания каждой лампы в течение года равна 0,2. Лампы перегорают независимо друг от друга. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит?
Решение:Всего — 3 лампочки.
противоположно тому, что ни одна не перегорит.
Ответ: 0.992Задание 5 (пример 2)
Текст задачи:В коробке 5 синих, 9 красных и 11 зелёных фломастеров. Случайным образом выбирают два фломастера. Найдите вероятность того, что окажутся выбраны один синий и один красный фломастеры.
Дано: Найти:Вероятность выбора 2 шт: 1 синий + 1 красный
Решение:- Если первым возьмут синий, а вторым возьмут красный фломастеры, то
- Если первым возьмут красный, а вторым возьмут синий фломастеры, то
-
Задание 6 (пример 1)
Текст задачи:Найдите корень уравнения
Решение: Ответ: 4Задание 6 (пример 2)
Текст задачи:Найдите корень уравнения
Решение: Ответ: 17Задание 6 (пример 3)
Текст задачи:Найдите корень уравнения
Решение: Ответ: 93Задание 6 (пример 4)
Текст задачи:Решите уравнение . Если корней окажется несколько, то в ответе запишите наименьший из них.
Решение:по теореме Виета
Ответ: 3Задание 7 (пример 1)
Текст задачи:Найдите значение выражения , если
Дано: Найти: Решение:Задание 7 (пример 2)
Текст задачи:Найдите значение выражения
Решение:
Задание 7 (пример 3)
Текст задачи:Найдите значение выражения
Решение:
Задание 8 (пример 1)
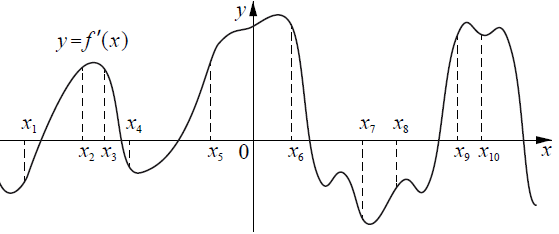
Текст задачи:На рисунке изображён график y = f'(x) производной функции f(x). На оси абсцисс отмечено десять точек: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10. Сколько из этих точек принадлежит промежуткам возрастания функции f(x)?
 Решение:
Решение:
f(x) возрастает ⇒ по рисунку f'(x) > 0 (график выше 0x) в точках: x2, x3, x5, x6, x9, x10. Таких точек 6.
Ответ: 6Задание 8 (пример 2)
Текст задачи:На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
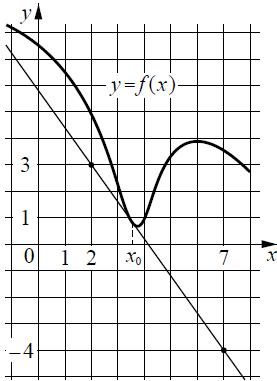 Решение:
Решение:
Пусть A(2; 3), B(7; -4), тогда
Задание 9
Текст задачи:Перед отправкой тепловоз издал гудок с частотой f0 = 295 Гц. Чуть позже гудок издал подъезжающий к платформе такой же тепловоз. Из-за эффекта Доплера частота второго гудка f (в Гц) больше первого: она зависит от скорости тепловоза v (в м/с) и изменяется по закону
(Гц), где c — скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 5 Гц. Определите,
с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а с = 300 м/с. Ответ дайте в м/с.
- ,
- Подставим числа
Задание 10 (пример 1)
Текст задачи:Моторная лодка прошла против течения реки 143 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
Решение:| по течению | 143 км | ||
| против течения | 143 км |
Задание 10 (пример 2)
Текст задачи:Смешав 45%-й и 97%-й растворы кислоты и добавив 10 кг чистой воды, получили 62%-й раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50%-го раствора той же кислоты, то получили бы 72%-й раствор кислоты. Сколько килограммов 45%-го раствора использовали для получения смеси?
Решение:| Раствор | m раствора | m кислоты | % |
|---|---|---|---|
| I | 45 | ||
| II | y | 97 | |
| III | 62 | ||
| IV | 72 |
- Вычтем , получим
Подставим в (1), получим:
Значит, 15кг 45% раствора использовали в смеси.
Ответ: 15Задание 10 (пример 3)
Текст задачи:Первая труба пропускает на 5 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 104 литра она заполняет на 5 минут дольше, чем вторая труба?
Решение:| Труба | Пропускная способность | Время | Работа |
|---|---|---|---|
| I | /мин | 104л | |
| II | 104л |
- НОЗ:
Значит, 8л/мин пропускает первая труба.
Ответ: 8Задание 11
Текст задачи:На рисунке изображены графики функций видов , пересекающиеся в точках A и B. Найдите абсциссу точки B.
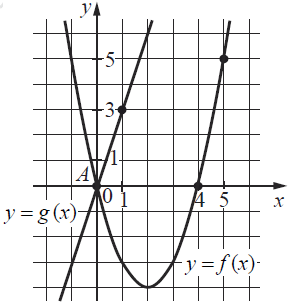 Дано:
Дано:
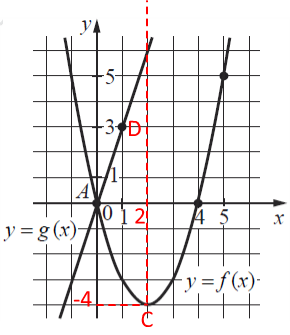
- Пусть вершина параболы, тогда
Задание 12 (пример 1)
Текст задачи:Найдите наименьшее значение функции на отрезке
Дано:на
Найти: Решение:Задание 12 (пример 2)
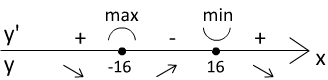
Текст задачи:Найдите точку максимума функции .
Дано:Задание 12 (пример 3)
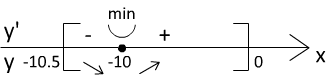
Текст задачи:Найдите точку минимума функции
Дано:Задания взяты из демонстрационного варианта для профильного уровня ЕГЭ по математике 2025 с сайта ФИПИ https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-2
Файлы для скачивания: