Задание №1
Пример №1
Треугольник ABC вписан в окружность с центром O. Угол BAC равен 32°. Найдите угол BOC. Ответ дайте в градусах.
Решение:
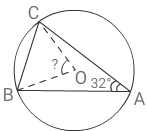
∠BAC =
12 ∠BOC (вписанный угол опирается на дугу BC) ⇒ ∠BOC = 2 × 32° = 64°
Ответ: 64
Пример №2
Площадь треугольника ABC равна 24; DE – средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.
Решение:
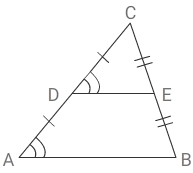
S
ABC = 24
S
CDE — ?
1) DE =
12AB (средняя линия треугольника)
2) Δ CDE ∼ Δ ABC (треугольники подобны по двум углам) ⇒
SCDESABC = k
2 = (
12)
2 =
14
SCDE24 =
14
S
CDE =
244 = 6
Ответ: 6
Пример №3
В ромбе ABCD угол DBA равен 13° . Найдите угол BCD. Ответ дайте в градусах.
Решение:
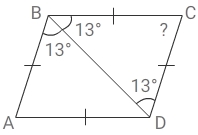
ABCD — ромб
1) ∠ DBA = 13° = ∠ CDB (н/л)
2) Δ DBC — равнобедренный треугольник с основанием BD ⇒ ∠ B = ∠ D = 13°
3) ∠ C = 180° — 2 × 13° = 180° — 26° = 154°
Ответ: 154
Пример №4
Стороны параллелограмма равны 24 и 27. Высота, опущенная на меньшую из этих сторон, равна 18. Найдите высоту, опущенную на бо́льшую сторону параллелограмма.
Решение:
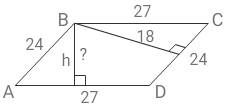
h — ?
S
ABCD = 24 × 18
S
ABCD = 27 × h
24 × 18 = 27 × h ⇒ h =
24 × 1827
h =
24 × 23 = 8 × 2 = 16
Ответ: 16
Задание №2
Пример №1
На координатной плоскости изображены векторы a
➔ и b
➔. Найдите скалярное произведение a
➔ × b
➔.
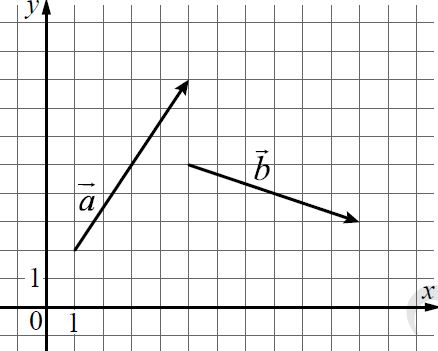 Решение:
Решение:
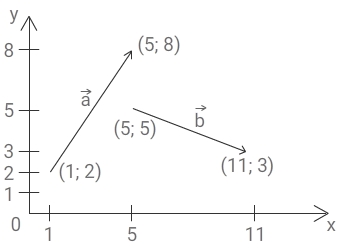
1) a
➔{5-1; 8-2}
a
➔{4; 6}
2) b
➔{11-5; 3-5}
b
➔{6; -2}
3) a
➔ × b
➔ = 4 × 6 + 6 × (-2) = 24 — 12 = 12
Ответ: 12
Пример №2
Даны векторы a
➔(1; 2), b
➔(-3; 6) и c
➔(4; -2). Найдите длину вектора a
➔ — b
➔ + c
➔.
Решение:
a
➔{1; 2}, b
➔{-3; 6}, c
➔{4; -2}
|a
➔ — b
➔ + c
➔| = ?
1) a
➔ — b
➔ {1-(-3); 2-6}
a
➔ — b
➔{4; -4}
2) a
➔ — b
➔ + c
➔ {4+4; -4-2}
a
➔ — b
➔ + c
➔ {8; -6}
3) |a
➔ — b
➔ + c
➔| = √
8² + (-6)² = √
100 = 10
Ответ: 10
Задание №3
Пример №1
В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором сосуде?
Ответ дайте в сантиметрах.
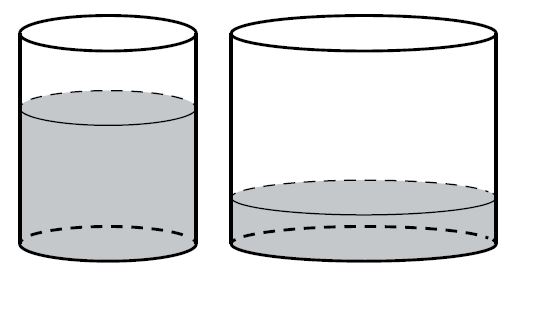 Решение:
Решение:
| Цилиндр |
I |
II |
| Высота |
16 |
h? |
| Диаметр |
d |
2d |
| Объем |
π(d2)2 × 16 |
π(2d2)2 × h |
V
ц = π
d24h
V
1 = V
2
π
d24 × 16 = πd
2h
h = 4
Ответ: 4
Пример №2
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь
боковой поверхности отсечённой треугольной призмы.
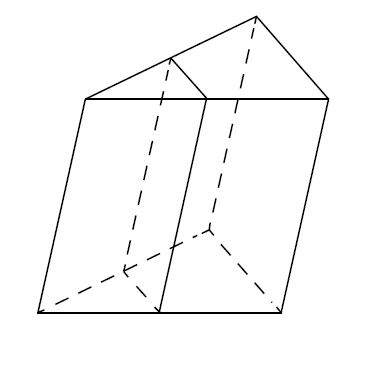 Решение:
Решение:
S
боковой поверхности призмы = 24
24 = P
основания × h
S
боковой поверхности отсеченной = ? =
12P
основания × h
S
боковой поверхности отсеченной =
12 × 24 = 12
Ответ: 12
Пример №3
Через точку, лежащую на высоте прямого кругового конуса и делящую её в отношении 1: 2 , считая от вершины конуса, проведена плоскость, параллельная его основанию и делящая конус на две части. Каков объём той части конуса, которая примыкает к его основанию, если объём всего конуса равен 54?
 Решение:
Решение:
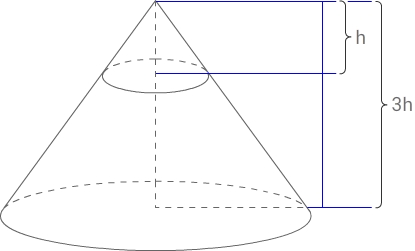
V
конуса = 54
V
нижнего конуса = ?
1)
Vверхнего конусаVнижнего конуса = (
h3h)
3
Vверхнего конуса54 = (
13)
3 =
127
2) V
нижнего конуса = 54 — 2 = 52
Ответ: 52
Задание №4
Пример №1
В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене выпускнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.
Решение:
n = 25
m = 2
p =
mn
p =
225 = 0.08
Ответ: 0.08
Пример №2
Вероятность того, что мотор холодильника прослужит более 1 года, равна 0,8, а вероятность того, что он прослужит более 2 лет, равна 0,6. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?
Решение:
P
>1 года = 0.8
P
>2 лет = 0.6
1 года < P < 2 лет
P = 0.8 — 0.6 = 0.2
Ответ: 0.2
Задание №5
Пример №1
Симметричную игральную кость бросили 3 раза. Известно, что в сумме выпало 6 очков. Какова вероятность события «хотя бы раз выпало 3 очка»?
Решение:
| Броски |
|
|
| I |
|
II |
|
III |
|
|
| 1 |
+ |
1 |
+ |
4 |
= |
6 |
| 1 |
+ |
4 |
+ |
1 |
= |
6 |
| 4 |
+ |
1 |
+ |
1 |
= |
6 |
| 2 |
+ |
2 |
+ |
2 |
= |
6 |
| 1 |
+ |
2 |
+ |
3 |
= |
6 |
| 1 |
+ |
3 |
+ |
2 |
= |
6 |
| 2 |
+ |
3 |
+ |
1 |
= |
6 |
| 2 |
+ |
1 |
+ |
3 |
= |
6 |
| 3 |
+ |
1 |
+ |
2 |
= |
6 |
| 3 |
+ |
2 |
+ |
1 |
= |
6 |
P хотя бы раз выпало 3 очка?
P =
610 = 0.6
Ответ: 0.6
Пример №2
В городе 48% взрослого населения – мужчины. Пенсионеры составляют 12,6% взрослого населения, причём доля пенсионеров среди женщин равна 15%. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».
Решение:
Всего взрослых — x человек, где 0.48x это мужчины ⇒ x — 0.48x = 0.52x это женщины.
Пенсионеры — 0.126x, где 0.126x — 0.078x = 0.048x это мужчины и 0.15 × 0.52x = 0.078x это женщины.
P =
0.0480.48 = 0.1
Ответ: 0.1
Задание №6
Пример №1
Найдите корень уравнения 3
x − 5 = 81.
Решение:
3
x − 5 = 81
3
x − 5 = 3
4
x — 5 = 4
x = 4 + 5
x = 9
Ответ: 9
Пример №2
Найдите корень уравнения √
3x + 49 = 10.
Решение:
√
3x + 49 = 10
3x + 49 = 10
2
3x + 49 = 100
3x = 100 — 49
3x = 51
x = 51 : 3 = 17
Ответ: 17
Пример №3
Найдите корень уравнения log
8(5x + 47) = 3.
Решение:
log
8(5x + 47) = 3
5x + 47 = 8
3 = 512
5x = 512 — 47 = 465
x = 465 : 5 = 93
Ответ: 93
Пример №4
Решите уравнение √
2x + 3 = x. Если корней окажется несколько, то в ответе запишите наименьший из них.
Решение:
√
2x + 3 = x, x ≥ 0
2x + 3 = x
2
x
2 — 2x — 3 = 0
x
1 = 3, x
2 = -1 посторонний корень
По теореме Виета

3 × (-1) = -3 = с
3 + (-1) = 2 = -b
Ответ: 3
Задание №7
Пример №1
Найдите sin 2α , если cosα = 0,6 и π < α < 2π.
Решение:
Дано: cosα = 0.6
π < α < 2π
Найти: sin2α
sin2α = 2sinα × cosα
1) sinα = -√
1 — 0.6² = -√
1 — 0.36
sinα = -√
0.64 = -0.8 т.к. α ∈ III — IV четверти, где sinα < 0
2) sin2α = 2 × (-0.8) × 0.6 = -0.96
Ответ: -0.96
Пример №2
Найдите значение выражения 16log
74√7
Решение:
16log
74√7 = 16 ×
14 × log
77 = 4 × 1 = 4
Ответ: 4
Пример №3
Найдите значение выражения
415 ×
16910
Решение:
415 ×
16910 =
415 × (
42)
910 =
415 ×
495 =
415 + 95 =
4105 =
42 =
16
Ответ: 16
Задание №8
Пример №1
На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x
1, x
2, … x
9.
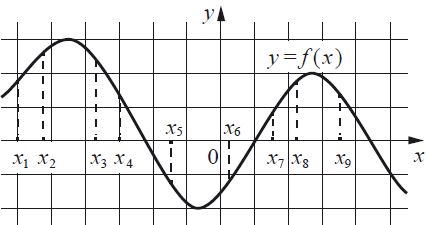
Найдите все отмеченные точки, в которых производная функции f(x) отрицательна. В ответе укажите количество этих точек.
Решение:
f'(x) < 0 ⇒ f(x) убывает в точках x
3, x
4, x
5, x
9 — 4 точки
Ответ: 4
Пример №2
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x
0. Найдите значение производной функции f(x) в точке x
0.
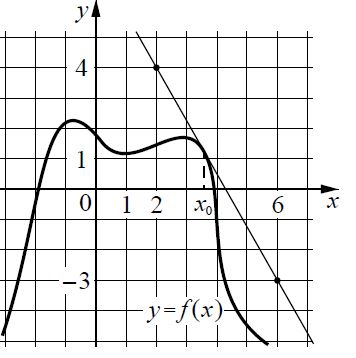 Решение:
Решение:
A(2; 4)
B(6; -3)
x
1 = 2 x
2 = 6
y
1 = 4 y
2 = -3
f'(x) =
ΔyΔx =
y2 — y1x2 — x1 =
-3 — 46 — 2 = —
74 = -1.75
Ответ: -1.75
Задание №9
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением
V = c ×
f — f0f + f0
где c =1500 м/с – скорость звука в воде, f0 – частота испускаемого сигнала (в МГц), f – частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.
Решение:
V = c ×
f — f0f + f0
f = ? МГц
f
0 = 749 МГц
V = 2 м/с c = 1500 м/с
2 = 1500 ×
f — 749f + 749
1750 =
f — 749f + 749
f + 749 = (f — 749) × 750
f + 749 = 750f — 749 × 750
750f — f = 749 + 749 × 750
749f = 749(1 + 750)
f = 751
Ответ: 751
Задание №10
Пример №1
Весной катер идёт против течения реки в 1
23 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1
12раза медленнее, чем по течению. Найдите скорость
течения весной (в км/ч).
Решение:
Пусть V
течения весной = x км/ч
V
собственная = y км/ч
| V |
Весна |
Лето |
| по течению |
y + x |
y + (x — 1) |
| против течения |
y — x |
y — (x — 1) |
V
против течения < V
по течению в 1
23 весной.
V
против течения < V
по течению в 1
12 летом.

1
23(y — x) = y + x
1
12(y — x + 1) = y + x — 1
 23
23y =
83x
12y +
52 =
52x

2y = 8x
y + 5 = 5x

y = 4x
y = 5x — 5
4x = 5x — 5
x = 5 км/ч
Ответ: 5
Пример №2
Смешав 45%-ный и 97%-ный растворы кислоты и добавив 10 кг чистой воды, получили 62%-ный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50%-ного раствора той же кислоты, то получили бы 72%-ный раствор кислоты. Сколько килограммов 45%-ного раствора использовали для получения смеси?
Решение:
| р/р |
m раствора |
m кислоты |
концентрация |
| I |
x ? |
0.45x |
45% |
| II |
y |
0.97y |
97% |
| III |
x + y + 10 |
0.45x + 0.97y + 0 |
62% |
| IV |
x + y + 10 |
0.45x + 0.97y + 0.5 × 10 |
72% |
1) Баланс по кислоте в III и IV

0.45x + 0.97y = 0.62(x + y + 10) (1)
0.45x + 0.97y + 5 = 0.72(x + y + 10) (2)
Вычтем (2) — (1), получим 0.1(x + y + 10) = 5
x + y + 10 = 50
x + y = 40 (*)
y = 40 — x
2) Подставим (*) в (1), получим
0.45x + 0.97(40 — x) = 0.62 × 50
0.45x + 38.8 — 0.97x = 31
0.52x = 7.8
x = 15 кг
Ответ: 15
Пример №3
Автомобиль, движущийся с постоянной скоростью 70 км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 40 км/ч. Каким будет расстояние (в километрах) между этими автомобилями через 15 минут после обгона?
Решение:
1) 70 — 40 = 30 (км/ч) — V
догона
2) 30 ×
1560 =
152 = 7.5 (км) — S
после обгона
Ответ: 7.5
Задание №11
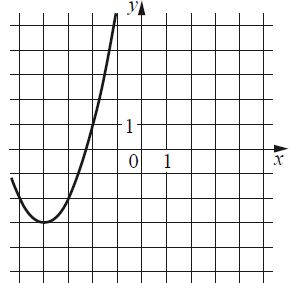
На рисунке изображён график функции вида f(x) = ax
2 + bx + c, где числа a, b и c — целые. Найдите значение f(−12).
 Решение:
Решение:
f(x) = ax
2 + bx + c f(-12) = ?
f(x) = a(x — x
0)
2 + y
0 где (x
0, y
0) вершина параболы
1) По рисунку x
0 = -4, y
0 = -3 тогда f(x) = a(x + 4)
2 — 3
Пусть A(-3; -2)
2) f(x) = a(-3 + 4)
2 — 3
-2 = a — 3 a = 1
3) f(x) = (x + 4)
2 — 3
4) f(-12) = (-12 + 4)
2 — 3
f(-12) = (-8)
2 — 3 = 64 — 3 = 61
Ответ: 61
Задание №12
Пример №1
Найдите наименьшее значение функции y = 9x − 9ln(x + 11) + 7 на отрезке [-10.5; 0].
Решение:
y = 9x — 9ln(x + 11) + 7
y
наименьшее = ? на [-10.5; 0]
x + 11 > 0, x > -11
1) y’ = 9 — 9 ×
1x + 11 = 9 × (1 —
1x + 11)
y’ = 9 ×
x + 10x + 11
y’ = 0 при
x + 10x + 11 = 0
x = -10
2)
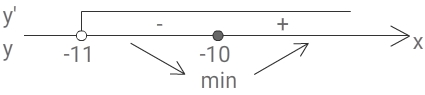
3) y
наименьшее = y(x
min) = y(-10) = 9 × (-10) — 9 × ln1 + 7 = -90 + 7 = -83
Ответ: -83
Пример №2
Найдите точку максимума функции y = (x+8)
2 × e
3-x
Решение:
x
max — ?
y = (x+8)
2 × e
3 — x
1) y’ = 2(x+8) × e
3 — x + (x+8)
2 × e
3 — x × (-1)
y’ = 2(x+8) × e
3 — x — (x+8)
2 × e
3 — x
y’ = (x+8) × e
3 — x × (2 — (x+8))
y’ = (x+8) × e
3 — x × (-x — 6) = 0
e
3 — x > 0 при ∀x ⇒ y’ = 0 при x + 8 = 0 или -x — 6 = 0
x
1 = -8 x = -6
2)

x
max = -6
Ответ: -6
Пример №3
Найдите точку минимума функции y = —
xx2 + 256
Решение:
x
min — ?
y’ = —
1 × (x2 + 256) — x × 2x(x2 + 256)2
y’ = —
x2 + 256 — 2x2(x2 + 256)2
y’ = —
-x2 + 256(x2 + 256)2 =
x2 — 256(x2 + 256)2
y’ = 0 при x
2 — 256 = 0
(x — 16)(x + 16) = 0
x
1 = 16 x
2 = -16

x
min = 16
Ответ: 16
Часть 2
Задание №13
Решите уравнение
а) 2sin(x +
π3) + cos2x = √
3cosx + 1
б) [-3π —
3π2]
Решение:
а) 2(sinx ×
π3) + cos2x = √
3cosx + 1
2(sinx ×
12 + cosx ×
√32) + cos2x = √
3cosx + 1
sinx + (cos2x — 1) = 0
sinx + (-2sin
2x) = 0
sinx(1 — 2sinx) = 0
sinx = 0
x = πn, n ∈ Z
или 1 — 2sinx = 0
sinx =
12

x =
π6 + 2πn, n ∈ Z
x =
5π6 + 2πn, n ∈ Z
б)
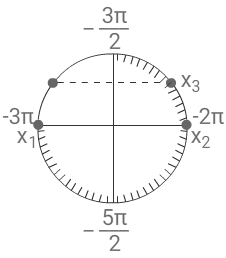
x
1 = -3π
x
2 = -2π
x
3 = -2π +
π6 = —
11π6
Ответ: a) πn;
π6 + 2πn;
5π6 + 2πn, n ∈ Z
б) -3π; -2π; —
11π6
Задание №14
В пирамиде ABCD рёбра DA, DB и DC попарно перпендикулярны, а AB = BC = AC = 5√2.
а) Докажите, что BD = CD.
б) На рёбрах DA и DC отмечены точки M и N соответственно, причём DM : MA = DN : NC = 2 : 3. Найдите площадь сечения MNB.
Решение:
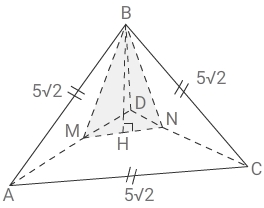
Дано: DABC — пирамида
DA ⊥ DB ⊥ DC
AB = BC = AC = 5√2
а) Доказать: BD = CD
б) Найти: S
сечения MNB
M ∈ DA, N ∈ DC
DMMA =
DNNC =
23
а) Доказательство:
Δ ABD = Δ ADC прямоугольные треугольники
AD — общий катет
AB = AC по условию ⇒ BD = CD что и требовалось доказать
б) 1) Δ BDC — прямоугольный, равнобедренный с основание BC.
Пусть BD = DC = x, тогда по теореме Пифагора x
2 + x
2 = (5√2)
2
2x
2 = 25 × 2
x
2 = 25
x = 5
Значит, BD = DC = 5
2) т.к. BA = BC — наклонные то DA = DC = 5 — проекции.
3) Δ BND (∠D = 90°)
BN = √
BD² + DN² = √
5² + 2² = √
29
т.к. DN =
25DC =
25 × 5 = 2
BN = BM = √
29 наклонные равных проекций
4) Δ MDN (∠D = 90°)
MN = √
MD² + DN² = √
2² + 2² = √8 = 2√2
5) BH — высота Δ MBN — равнобедренный ⇒ BH — медиана ⇒ MH =
12MN
MH =
12 × 2√2 = √2
6) S
сечения = S
MBN =
12MN × BH =
12 × 2√2 × BH = √
2×BH
7) Δ MBH (∠H = 90°)
BH = √
BM² — MH² = √
(√29)² — (√2)²
BH = √
29 — 2 = √
27 = 3√3
8 ) S
MBH = √
2 × 3√
3 = 3√
6
Ответ: 3√6
Задание №15
Решите неравенство log
11(8x
2 + 7) — log
11(x
2 + x + 1) ≥ log
11(
xx + 5 + 7)
Решение:
1) 8x
2 + 7 > 0 при ∀ x
x
2 + x + 1 > 0 при ∀ x
т.к. D = 1 — 4 = -3 < 0 и a = 1 > 0
2) log
118x2 + 7x2 + x + 1 ≥ log
11(
xx + 5 + 7)
 xx + 5
xx + 5 + 7 > 0 (1)
8x2 + 7x2 + x + 1 ≥
xx + 5 + 7 (2)
3) Решим (1) неравенство системы
x + 7x + 35x + 5 > 0
8x + 35x + 5 > 0
8x + 35 = 0
x = —
358 = -4
38
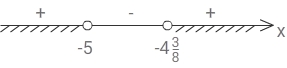
x ∈ (-∞; -5) ∪ (-4
38; +∞) (*)
4) Решим (2) неравенство системы
8x2 + 7x2 + x + 1 ≥
8x + 35x + 5
(8x2 + 7)(x + 5) — (8x + 35)(x2 + x + 1)(x2 + x + 1)(x + 5) ≥ 0
8x3 + 40x2 + 7x + 35 — 8x3 — 8x2 — 8x — 35x2 — 35x — 35(x2 + x + 1)(x + 5) ≥ 0
-3x2 — 36x(x2 + x + 1)(x + 5) ≥ 0 | :(-3)
x2 + 12x(x2 + x + 1)(x + 5) ≤ 0 | ×(x
2 + x + 1 > 0)
x(x +12)x + 5 ≤ 0
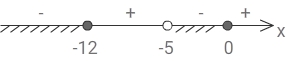
x ∈ (-∞; -12] ∪ (-5; 0] (**)
5) Совместим (*) и (**)
 Ответ:
Ответ: (-∞; -12] ∪ (-4
38; 0]
Задание №16
В июле 2025 года планируется взять кредит на десять лет в размере 800 тыс. рублей. Условия его возврата таковы:
– каждый январь долг будет возрастать на r% по сравнению с концом предыдущего года (r – целое число);
– с февраля по июнь каждого года необходимо оплатить одним платежом часть долга;
– в июле 2026, 2027, 2028, 2029 и 2030 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года;
– в июле 2030 года долг должен составить 200 тыс. рублей;
– в июле 2031, 2032, 2033, 2034 и 2035 годов долг должен быть на другую одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2035 года долг должен быть выплачен полностью.
Известно, что сумма всех платежей после полного погашения кредита будет равна 1480 тыс. рублей. Найдите r.
Решение:
1) (800000 — 200000) : 5 лет = 120000 выплаты с 2026 год по 2030 год
2) 200000 : 5 = 40000 выплаты с 2031 года по 2035 год
3) 1 + 0.01r = k
| Год |
Долг в июле |
Долг в январе |
Выплаты |
| 2025 |
800000 |
800000 + 800000×0.01 = 800000k |
800000k — 680000 |
| 2026 |
800000 — 120000 = 680000 |
680000k |
680000k — 560000 |
| 2027 |
680000 — 120000 = 560000 |
560000k |
560000k — 440000 |
| 2028 |
560000 — 120000 = 440000 |
440000k |
440000k — 320000 |
| 2029 |
440000 — 120000 = 320000 |
320000k |
320000k — 200000 |
| 2030 |
320000 — 120000 = 200000 |
200000k |
200000k — 160000 |
| 2031 |
200000 — 40000 = 160000 |
160000k |
160000k — 120000 |
| 2032 |
160000 — 40000 = 120000 |
120000k |
120000k — 80000 |
| 2033 |
120000 — 40000 = 80000 |
80000k |
80000k — 40000 |
| 2034 |
80000 — 40000 = 40000 |
40000k |
40000k — 0 |
| 2035 |
40000 — 40000 = 0 |
0k |
|
Сумма всех платежей 1480 тысяч рублей
3400000k — 2600000 = 1480000
3400000k = 4080000
k = 1.2
1 + 0.01r = 1.2
0.01r = 0.2
r = 20
Ответ: 20%
Задания взяты из демонстрационного варианта для профильного уровня ЕГЭ по математике 2024 с сайта ФИПИ https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-2
Файлы для скачивания:
- Демонстрационный вариант для профильного уровня Скачать
- Спецификация для профильного уровня Скачать
- Кодификатор Скачать
 ∠BAC = 12 ∠BOC (вписанный угол опирается на дугу BC) ⇒ ∠BOC = 2 × 32° = 64°
Ответ: 64
∠BAC = 12 ∠BOC (вписанный угол опирается на дугу BC) ⇒ ∠BOC = 2 × 32° = 64°
Ответ: 64
 SABC = 24
SCDE — ?
1) DE = 12AB (средняя линия треугольника)
2) Δ CDE ∼ Δ ABC (треугольники подобны по двум углам) ⇒ SCDESABC = k2 = (12)2 = 14
SCDE24 = 14
SCDE = 244 = 6
Ответ: 6
SABC = 24
SCDE — ?
1) DE = 12AB (средняя линия треугольника)
2) Δ CDE ∼ Δ ABC (треугольники подобны по двум углам) ⇒ SCDESABC = k2 = (12)2 = 14
SCDE24 = 14
SCDE = 244 = 6
Ответ: 6
 ABCD — ромб
1) ∠ DBA = 13° = ∠ CDB (н/л)
2) Δ DBC — равнобедренный треугольник с основанием BD ⇒ ∠ B = ∠ D = 13°
3) ∠ C = 180° — 2 × 13° = 180° — 26° = 154°
Ответ: 154
ABCD — ромб
1) ∠ DBA = 13° = ∠ CDB (н/л)
2) Δ DBC — равнобедренный треугольник с основанием BD ⇒ ∠ B = ∠ D = 13°
3) ∠ C = 180° — 2 × 13° = 180° — 26° = 154°
Ответ: 154
 h — ?
SABCD = 24 × 18
SABCD = 27 × h
24 × 18 = 27 × h ⇒ h = 24 × 1827
h = 24 × 23 = 8 × 2 = 16
Ответ: 16
h — ?
SABCD = 24 × 18
SABCD = 27 × h
24 × 18 = 27 × h ⇒ h = 24 × 1827
h = 24 × 23 = 8 × 2 = 16
Ответ: 16
 Решение:
Решение:
 1) a➔{5-1; 8-2}
a➔{4; 6}
2) b➔{11-5; 3-5}
b➔{6; -2}
3) a➔ × b➔ = 4 × 6 + 6 × (-2) = 24 — 12 = 12
Ответ: 12
1) a➔{5-1; 8-2}
a➔{4; 6}
2) b➔{11-5; 3-5}
b➔{6; -2}
3) a➔ × b➔ = 4 × 6 + 6 × (-2) = 24 — 12 = 12
Ответ: 12
 Решение:
Решение:
 Решение:
Sбоковой поверхности призмы = 24
24 = Pоснования × h
Sбоковой поверхности отсеченной = ? = 12Pоснования × h
Sбоковой поверхности отсеченной = 12 × 24 = 12
Ответ: 12
Решение:
Sбоковой поверхности призмы = 24
24 = Pоснования × h
Sбоковой поверхности отсеченной = ? = 12Pоснования × h
Sбоковой поверхности отсеченной = 12 × 24 = 12
Ответ: 12
 Решение:
Решение:
 Vконуса = 54
Vнижнего конуса = ?
1) Vверхнего конусаVнижнего конуса = (h3h)3
Vверхнего конуса54 = (13)3 = 127
2) Vнижнего конуса = 54 — 2 = 52
Ответ: 52
Vконуса = 54
Vнижнего конуса = ?
1) Vверхнего конусаVнижнего конуса = (h3h)3
Vверхнего конуса54 = (13)3 = 127
2) Vнижнего конуса = 54 — 2 = 52
Ответ: 52
 Найдите все отмеченные точки, в которых производная функции f(x) отрицательна. В ответе укажите количество этих точек.
Решение:
f'(x) < 0 ⇒ f(x) убывает в точках x3, x4, x5, x9 — 4 точки
Ответ: 4
Найдите все отмеченные точки, в которых производная функции f(x) отрицательна. В ответе укажите количество этих точек.
Решение:
f'(x) < 0 ⇒ f(x) убывает в точках x3, x4, x5, x9 — 4 точки
Ответ: 4
 Решение:
A(2; 4)
B(6; -3)
x1 = 2 x2 = 6
y1 = 4 y2 = -3
f'(x) = ΔyΔx = y2 — y1x2 — x1 = -3 — 46 — 2 = —74 = -1.75
Ответ: -1.75
Решение:
A(2; 4)
B(6; -3)
x1 = 2 x2 = 6
y1 = 4 y2 = -3
f'(x) = ΔyΔx = y2 — y1x2 — x1 = -3 — 46 — 2 = —74 = -1.75
Ответ: -1.75
 Решение:
f(x) = ax2 + bx + c f(-12) = ?
f(x) = a(x — x0)2 + y0 где (x0, y0) вершина параболы
1) По рисунку x0 = -4, y0 = -3 тогда f(x) = a(x + 4)2 — 3
Пусть A(-3; -2)
2) f(x) = a(-3 + 4)2 — 3
-2 = a — 3 a = 1
3) f(x) = (x + 4)2 — 3
4) f(-12) = (-12 + 4)2 — 3
f(-12) = (-8)2 — 3 = 64 — 3 = 61
Ответ: 61
Решение:
f(x) = ax2 + bx + c f(-12) = ?
f(x) = a(x — x0)2 + y0 где (x0, y0) вершина параболы
1) По рисунку x0 = -4, y0 = -3 тогда f(x) = a(x + 4)2 — 3
Пусть A(-3; -2)
2) f(x) = a(-3 + 4)2 — 3
-2 = a — 3 a = 1
3) f(x) = (x + 4)2 — 3
4) f(-12) = (-12 + 4)2 — 3
f(-12) = (-8)2 — 3 = 64 — 3 = 61
Ответ: 61
 3) yнаименьшее = y(xmin) = y(-10) = 9 × (-10) — 9 × ln1 + 7 = -90 + 7 = -83
Ответ: -83
3) yнаименьшее = y(xmin) = y(-10) = 9 × (-10) — 9 × ln1 + 7 = -90 + 7 = -83
Ответ: -83
 xmax = -6
Ответ: -6
xmax = -6
Ответ: -6
 xmin = 16
Ответ: 16
xmin = 16
Ответ: 16
 x1 = -3π
x2 = -2π
x3 = -2π + π6 = —11π6
Ответ: a) πn; π6 + 2πn; 5π6 + 2πn, n ∈ Z
б) -3π; -2π; —11π6
x1 = -3π
x2 = -2π
x3 = -2π + π6 = —11π6
Ответ: a) πn; π6 + 2πn; 5π6 + 2πn, n ∈ Z
б) -3π; -2π; —11π6
 Дано: DABC — пирамида
DA ⊥ DB ⊥ DC
AB = BC = AC = 5√2
а) Доказать: BD = CD
б) Найти: Sсечения MNB
M ∈ DA, N ∈ DC
DMMA = DNNC = 23
а) Доказательство:
Δ ABD = Δ ADC прямоугольные треугольники
AD — общий катет
AB = AC по условию ⇒ BD = CD что и требовалось доказать
б) 1) Δ BDC — прямоугольный, равнобедренный с основание BC.
Пусть BD = DC = x, тогда по теореме Пифагора x2 + x2 = (5√2)2
2x2 = 25 × 2
x2 = 25
x = 5
Значит, BD = DC = 5
2) т.к. BA = BC — наклонные то DA = DC = 5 — проекции.
3) Δ BND (∠D = 90°)
BN = √BD² + DN² = √5² + 2² = √29
т.к. DN = 25DC = 25 × 5 = 2
BN = BM = √29 наклонные равных проекций
4) Δ MDN (∠D = 90°)
MN = √MD² + DN² = √2² + 2² = √8 = 2√2
5) BH — высота Δ MBN — равнобедренный ⇒ BH — медиана ⇒ MH = 12MN
MH = 12 × 2√2 = √2
6) Sсечения = SMBN = 12MN × BH = 12 × 2√2 × BH = √2×BH
7) Δ MBH (∠H = 90°)
BH = √BM² — MH² = √(√29)² — (√2)²
BH = √29 — 2 = √27 = 3√3
8 ) SMBH = √2 × 3√3 = 3√6
Ответ: 3√6
Дано: DABC — пирамида
DA ⊥ DB ⊥ DC
AB = BC = AC = 5√2
а) Доказать: BD = CD
б) Найти: Sсечения MNB
M ∈ DA, N ∈ DC
DMMA = DNNC = 23
а) Доказательство:
Δ ABD = Δ ADC прямоугольные треугольники
AD — общий катет
AB = AC по условию ⇒ BD = CD что и требовалось доказать
б) 1) Δ BDC — прямоугольный, равнобедренный с основание BC.
Пусть BD = DC = x, тогда по теореме Пифагора x2 + x2 = (5√2)2
2x2 = 25 × 2
x2 = 25
x = 5
Значит, BD = DC = 5
2) т.к. BA = BC — наклонные то DA = DC = 5 — проекции.
3) Δ BND (∠D = 90°)
BN = √BD² + DN² = √5² + 2² = √29
т.к. DN = 25DC = 25 × 5 = 2
BN = BM = √29 наклонные равных проекций
4) Δ MDN (∠D = 90°)
MN = √MD² + DN² = √2² + 2² = √8 = 2√2
5) BH — высота Δ MBN — равнобедренный ⇒ BH — медиана ⇒ MH = 12MN
MH = 12 × 2√2 = √2
6) Sсечения = SMBN = 12MN × BH = 12 × 2√2 × BH = √2×BH
7) Δ MBH (∠H = 90°)
BH = √BM² — MH² = √(√29)² — (√2)²
BH = √29 — 2 = √27 = 3√3
8 ) SMBH = √2 × 3√3 = 3√6
Ответ: 3√6
 x ∈ (-∞; -5) ∪ (-438; +∞) (*)
4) Решим (2) неравенство системы
8x2 + 7x2 + x + 1 ≥ 8x + 35x + 5
(8x2 + 7)(x + 5) — (8x + 35)(x2 + x + 1)(x2 + x + 1)(x + 5) ≥ 0
8x3 + 40x2 + 7x + 35 — 8x3 — 8x2 — 8x — 35x2 — 35x — 35(x2 + x + 1)(x + 5) ≥ 0
-3x2 — 36x(x2 + x + 1)(x + 5) ≥ 0 | :(-3)
x2 + 12x(x2 + x + 1)(x + 5) ≤ 0 | ×(x2 + x + 1 > 0)
x(x +12)x + 5 ≤ 0
x ∈ (-∞; -5) ∪ (-438; +∞) (*)
4) Решим (2) неравенство системы
8x2 + 7x2 + x + 1 ≥ 8x + 35x + 5
(8x2 + 7)(x + 5) — (8x + 35)(x2 + x + 1)(x2 + x + 1)(x + 5) ≥ 0
8x3 + 40x2 + 7x + 35 — 8x3 — 8x2 — 8x — 35x2 — 35x — 35(x2 + x + 1)(x + 5) ≥ 0
-3x2 — 36x(x2 + x + 1)(x + 5) ≥ 0 | :(-3)
x2 + 12x(x2 + x + 1)(x + 5) ≤ 0 | ×(x2 + x + 1 > 0)
x(x +12)x + 5 ≤ 0
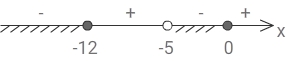 x ∈ (-∞; -12] ∪ (-5; 0] (**)
5) Совместим (*) и (**)
x ∈ (-∞; -12] ∪ (-5; 0] (**)
5) Совместим (*) и (**)
 Ответ: (-∞; -12] ∪ (-438; 0]
Ответ: (-∞; -12] ∪ (-438; 0]





