Вариант 2, решение и ответы (ЕГЭ 2024 математика профильный уровень Ященко 36 вариантов ФИПИ)

Часть 1

Задание 1

Решение: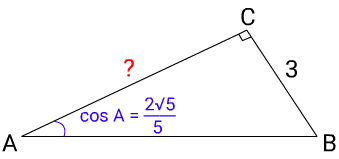 1) sinA = √1 — cos²A sinA = √(1 — (2√55)²) sinA = √(1 — 2025) = √(1 — 45) = √15 = 1√5 2) tgA = sinAcosA = 1√5 : 2√55 = 1√5 × 52√5 tgA = 12 3) tgA = BCAC = 3AC 12 = 3AC AC = 2 × 3 = 6 Ответ: 6

---

Задание 2

Решение:

Вектор	Начало	Конец	Координаты вектора
a➔	(-6; 4)	(-2; -2)	{-2 + 6; -6} = {4; -6}
b➔	(-1; -4)	(2; 3)	{2 + 1; 3 + 4} = {3; 7}

2a➔{2 × 4; 2 × (-6)} = {8; -12} b➔{3; 7} 2a➔ × b➔ = 8 × 3 — 12 × 7 = 24 — 84 = -60 Ответ: -60

---

Задание 3

V_{воды было} = 6 см³ h — высота была V_{воды стало} = ? см³ 1.6h — высота стала ΔV — ? Решение: 1) S_{основания цилиндрического сосуда} × h = 6 первоначально 2) S_{основания цилиндрического сосуда} × 1.6h = 6 × 1.6 = 9.6 3) ΔV = 9.6 — 6 = 3.6 см³ объем детали Ответ: 3.6 см³

---

Задание 4

Уругвай — 8 человек Чили — 7 человек Парагвай — 5 человек Решение: P_Чили = 78 + 7 + 5 = 720 = 0.35 Ответ: 0.35

---

Задание 5

1 полка: 25 блюдец = 16 красных + 9 синих 2 полка: 25 чашек = 13 красных + 12 синих Решение:

	Синие	Красные	Всего
Блюдца	9	16	25
Чашки	12	13	25

1) Одна чайная пара синего цвета P₁ = (925 × 1224) × (1225 × 1124) = 3 × 112 × 25 × 25 2) Одна чайная пара красного цвета P₂ = (1625 × 1524) × (1325 × 1224) = 135 × 25 3) Две чайные пары разных цветов P₃ = 2 × (1625 × 924) × 2 × (1325 × 1224) = 4 × 3 × 1325 × 25 4) P = P₁ + P₂ + P₃ P = 3 × 11 + 13 × 10 + 4 × 3 × 13 × 22 × 25 × 25 = 0.38 Ответ: 0.38

Задание 6

Решение:

2^{log₁₆(5x + 4)} = 5 2^{log₁₆(5x + 4)} = 2^log₂5 log₁₆(5x + 4) = log₂5 log_2⁴(5x + 4)¹ = log₂5 14log₂(5x + 4) = log₂5 умножим обе части равенства на 4 log₂(5x + 4) = 4log₂5 log₂(5x + 4) = log₂5⁴ 5x + 4 = 625 5x = 621 x = 124.2 Ответ: 124.2

---

Задание 7

Решение: (125⁷)³ : (25⁴)⁸ = 5^3×7×3 : 5^2×4×8 = 5⁶³ : 5⁶⁴ = 5^63-64 = 5^-1 = 15 = 0.2 Ответ: 0.2

---

Задание 8

Решение: f(x) убывает ⇒ f'(x) < 0, x ∈ Z
f'(x) < 0 при x₁ = -6, x₂ = -5, x₃ = -4, x₄ = -1, x₅ = 1, x₆ = 2 Сумма этих чисел -6 + (-5) + (-4) + (-1) + 1 + 2 = -13 Ответ: -13

---

Задание 9

H(t) = H₀ — √2gH₀ × kt + g2k²t² H₀ = 20 м k = 1200 g = 10 м/c² t — ?с 14H₀ останется Решение: 14H₀ = H₀ — √2 × 10 × 20 × 1200t + 102 × (1200)²t² 14 × 20 = 20 — √400 × 1200t + 5 × 140000t² 5 = 20 — 20200t + 18000t² 18000t² — 110t + 15 = 0 умножим обе части уравнения на 8000 t² — 800t + 120000 = 0 D4 = 160000 — 120000 = 40000 = 200² t_1,2 = 400 ± 200 t₁ = 400 — 200 = 200 секунд — меньшее время t₂ = 400 + 200 = 600 секунд Через 400 секунд воды в баке не останется т.е. H = 0 400с < 600с
Ответ: 200

---

Задание 10

Решение:

	P	t	A
I	(x — 2)л/мин	120x — 2	120л
II	x ?л/мин	120x	120л

t₂ < t₁ на 2 минуты t₁ — t₂ = 2 мин 120x — 2 — 120x = 2 120x — 120(x — 2) = 2x(x — 2) 120x — 120x + 240 = 2x² — 4x 2x² — 4x — 240 = 0 разделим на 2 обе части уравнения x² — 2x — 120 = 0 D4 = 1 + 120 = 121 = 11² x_1,2 = 1 ± 11 x₁ = 1 + 11 = 12(л/мин) x₂ = 1 — 11 = -10 что меньше 0 Ответ: 12

---

Задание 11

Решение: x — ? f(x) = 8 Пусть A(2; 1), B(-3; 3) f(x) = kx + b — линейная функция 1) Подставим координаты точек в формулу, получим систему 1 = k × 2 + b 3 = k × (-3) + b 2k + b = 1 (1) -3k + b = 3 (2) Вычтем (2) — (1) -5k = 2 ⇒ k = —25 = -0.4 Подставим k = -0.4 в (1), получим 2 × (-0.4) + b = 1 b = 0.8 + 1 b = 1.8 2) Составим функцию f(x) = -0.4x + 1.8 3) Найдем x при котором f(x) = 8 8 = -0.4x + 1.8 0.4x = -8 + 1.8 0.4x = -6.2 x = -15.5 Ответ: -15.5

---

Задание 12

x_max — ? y = (x — 14)²e^26-x Решение: y’ = 2(x — 14) × e^26-x — (x — 14)² × e^26-x y’ = (x — 14) × e^26-x × (2 — (x — 14)) y’ = (x — 14) × e^26-x × (2 — x + 14) y’ = (x — 14) × e^26-x × (-x + 16) y’ = 0 при (x — 14)(-x + 16) = 0, e^26-x > 0 x₁ = 14 x₂ = 16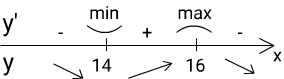 X_max = 16 Ответ: 16

---

Часть 2

Задание 13

Решение: sin²x + cosx — cosx × cos2x = 0 sin²x + cosx(1 — cos2x) = 0 sin²x + cosx × 2sin²x = 0 sin²x(1 + 2cosx) = 0

sin2x = 0	или	1 + 2cosx = 0
1 — cos2x2 = 0 1 — cos2x = 0 cos2x = 1 2x = 2πn, n ∈ Z x = πn, n ∈ Z x1 = -2π x2 = -π — π3 = —4π3 x3 = -π		2cosx = -1 cosx = —12 x = —2π3 + 2πn, n ∈ Z x = 2π3 + 2πn, n ∈ Z

Ответ: a) πn, n ∈ Z ±2π3 + 2πn, n ∈ Z б) -2π; —4π3; -π

---

Задание 14

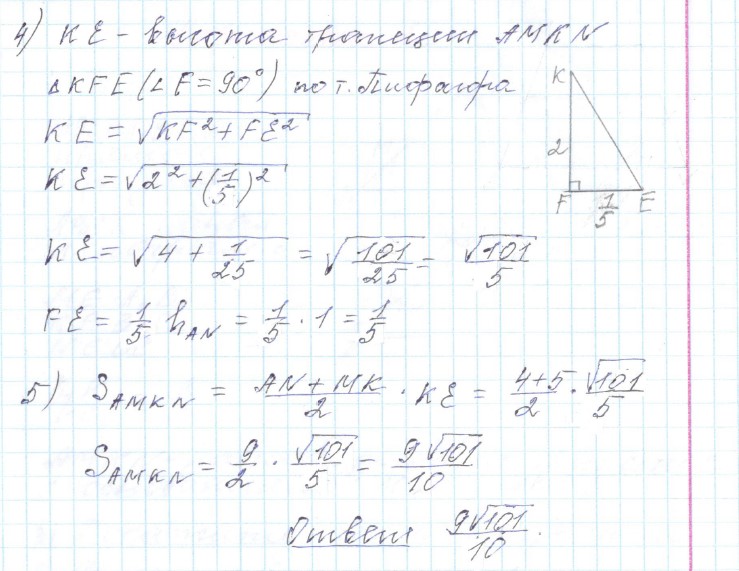
Задание 15

Решение:

3^{2√x — 10} + 6561 × 12^{√x — 4} < 3^2√x + 16 × 12^{√x — 6} 6561 × 12^√x × 12^-4 — 16 × 12^√x × 12^-6 < 3^2√x — 3^2√x × 3^-10 12^√x × 12^-4(3⁸ — 4² × 12^-2) < 3^2√x(1 — 3^-10) 12^√x × 12^-4(3⁸ — 4² × 3^-2 × 4^-2) < 3^2√x(1 — 3^-10) 12^√x × 12^-4 × 3⁸(1 — 3^-10) < 3^2√x(1 — 3^-10) 12^√x × 12^-4 × 3⁸ < 3^2√x 12^√x × 3^-4 × 4^-4 × 3⁸ < (3²)^√x 12^√x × (34)⁴ > 9^√x разделим обе части неравенства на 9^√x > 0 (129)^√x × (34)⁴ < 1 разделим обе части неравенства на (34)⁴ (43)^√x < (43)⁴ ⟺ x ≥ 0 √x < 4
x ≥ 0 x < 16 Ответ: [0; 16)