Вариант 1, решение заданий с ответами - Ященко ЕГЭ 2024 математика профильный уровень 36 вариантов ФИПИ

Часть 1

Задание 1

Решение: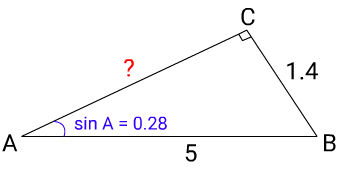

1) sin A = BCAB 0.28 = BC5 BC = 0.28 × 5 = 1.4 2) по теореме Пифагора AC = √5² — 1.4² = √25 — 1.96 AC = √23.04 = 4.8 Ответ: 4.8

Задание 2

a^➔ = AA₁^➔, A(-2; 5), A₁(-6; -4) b^➔ = BB₁^➔, B(6; 2), B₁(1; -2) Решение: 1) AA₁^➔{-6-(-2); -4-5} = {-4; -9} BB₁^➔{1-6; -2-2} = {-5; -4} 2) 2b^➔ = 2 × BB₁^➔{-5×2; 2×(-4)} = {-10; -8} 3) a^➔ × 2b^➔ = -4 × (-10) + (-9) × (-8) = 40 + 72 = 112 Ответ: 112

Задание 3

Решение: V_{цилиндра} = πR²h V₁ = πR² × 20 2100 = πR² × 20 πR² = 210020 = 105 V₂ = πR² × (20 + 5) = πR² × 25 = 105 × 25 = 2625 _ΔV = 2625 — 2100 = 525 Ответ: 525

Задание 4

Решение: P_{из Индии} = количество из Индииколичество всех участников = 75 + 4 + 9 + 7 = 725 = 28100 = 0.28 Ответ: 0.28

Задание 5

	Синие	Красные
Блюдца	14	22
Чашки	27	9

Решение: Блюдец 14 + 22 = 36 Чашек 27 + 9 = 36 1) Одна чайная пара синего цвета: (1436 × 1335) × (2736 × 2635) 2) Одна чайная пара красного цвета: (2236 × 2135) × (936 × 835) 3) Две чайные пары разных цветов: 2 × (2236 × 1435) × 2 × (936 × 2735) 4) P_{2 пары одного цвета} = 1436 × 1335 × 2736 × 2635 + 2236 × 2135 × 936 × 835 + 2 2236 × 1435 × 936 × 2735 = 14 × 13 × 27 × 2636 × 35 × 36 × 35 + 22 × 21 × 9 × 836 × 35 × 36 × 35 + 4 × 22 × 14 × 9 × 2736 × 35 × 36 × 35 = 13 × 133 × 35 × 4 × 5 + 11 × 25 × 6 × 35 + 11 × 335 × 5 = 169 + 44 + 39635 × 5 × 3 × 4 = 60935 × 5 × 3 × 4 = 203700 = 0.29 Ответ: 0.29

Задание 6

Решение:

3^{log₂₇(8x + 4)} = 4 3^{log_3³(8x + 4)} = 4 3^{13log₃(8x + 4)} = 4 (3^{log₃(8x + 4)})¹³ = 4 (8x + 4)¹³ = 4 ³√8x + 4 = 4 8x + 4 = 4³ 8x = 64 — 4 8x = 60 x = 608 = 152 = 7.5 Ответ: 7.5

Задание 7

Решение: (8⁵)³ : (4²)⁹ = 8¹⁵ : 4¹⁸ = (2³)¹⁵ : (2²)¹⁸ = 2⁴⁵ : 2³⁶ = 2^45-36 = 2⁹ = 512 Ответ: 512

Задание 8

Решение: f(x) возрастает там где f(x) > 0 Сумма целых чисел -4 + (-3) + (-2) + (-1) + 0 + 1 + 2 = -7 Ответ: -7

Задание 9

H(t) = H₀ — √2gH₀ × kt + g2k²t² t — ? Решение: V_{остатка воды} = 14V₀ ⇒ H_{остатка воды} = 14H₀ V ∼ H Подставим в формулу данные числовые значения: 14H₀ = 5 — √2 × 10 × 5 × 1700t + 102(1700)²t² 14 × 5 = 5 — √100 × 1700t + 5 × 149 × 10⁴t² 54 = 5 — 10700t + 5490000t² разделим обе части уравнения на 5 14 = 1 — 2700t + 1490000t² 1490000t² — 1350t + 34 = 0 умножим обе части равенства на 490000 t² — 1400t + 367500 = 0 D4 = 700² — 367500 = 490000 — 367500 D4 = 122500 = 350² t_1,2 = 700 ± 350 t₁ = 700 — 350 = 350 t₂ = 700 + 350 = 1050 не удовлетворяет условию задачи т.к. за 350 секунд вытекло из бака 3/4 объема воды, следовательно за 1050 секунд воды в баке останется точно меньше чем 1/4 от первоначального объема. Ответ: 350

Задание 10

Решение:

	P	t	A
I	x?	621x	621
II	x + 4	486x + 4	486

t₁ > t₂ на 9 минут t₁ — t₂ = 9 621x — 486x + 4 = 9 умножим обе части уравнения на x(x+4) 621(x + 4) — 486x = 9x(x + 4) 621x + 621 × 4 — 486x = 9x² + 36x 9x² + 36x + 486x — 621x — 621 × 4 = 0 9x² — 99x — 2484 = 0 x² — 11x — 276 = 0 D = 121 + 4276 = 121 + 1104 = 1225 = 35² x_1,2 = 11 ± 352 x₁ = 11 + 352 = 462 = 23 x₂ = 11 — 352 = -12 что меньше 0 Ответ: 23

Задание 11

f(x) = ax + b f(11) — ? Решение: По рисунку A(1; -3) B(5; 2) Подставим координаты точек в функцию

-3 = a × 1 + b 2 = a × 5 + b

a = -b — 3 2 = (-b — 3) × 5 + b 2 = -5b — 15 + b 17 = -4b b = — 174 ⇒ a = -(-174) — 3 a = 174 — 3 = 414 — 3 = 114 Составим функцию f(x) = 114x — 414 f(11) = 114 × 11 — 414 f(11) = 54 × 11 — 174 = 554 — 174 = 384 f(11) = 9.5 Ответ: 9.5

Задание 12

y_{наименьшее} — ? на отрезке [-1; 7] Решение: 1) y’ = (x² — 10x + 10)’ × e^2-x + (x² — 10x + 10) × (e^2-x)’ = (2x — 10) × e^2-x + (x² — 10x + 10) × e^2-x × (-1) = (2x — 10) × e^2-x — (x² — 10x + 10) × e^2-x = e^2-x × ((2x — 10) — (x² — 10x + 10)) = e^2-x × (2x — 10 — x² + 10x — 10) = e^2-x × (-x² + 12x — 20) 2) y’ = 0 при -x² + 12x — 20 = 0 e^2-x > 0 при ∀ x y’ = -x² + 12x — 20 x² — 12x + 20 = 0 По теореме Виета подбором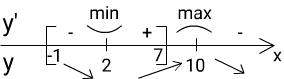

x₁ + x₂ = 12 x₁ × x₂ = 20

x₁ = 2 x₂ = 10

Задание 12 вариант 1 ЕГЭ 2024 математика профиль

y’ = -(x — 2)(x — 10) На [-1; 7] единственная точка экстремума и она минимум ⇒ в ней функция принимает наименьшее значение y_{наименьшее} = y(X_min) = y(2) = (2² — 10 × 2 + 10) × e^2-2 = -6 × e⁰ = -6 × 1 = -6 Ответ: -6

Часть 2

Задание 13

Решение: sinx × cos2x — √3cos²x + sinx = 0 а) sinx × cos2x — √3 × 1 + cos2x2 + sinx = 0 (sinx × cos2x + sinx) — √32(1 + cos2x) = 0 sinx(cos2x + 1) — √32(1 + cos2x) = 0 (cos2x + 1)(sinx — √32) = 0 cos2x + 1 = 0 cos2x = -1 2x = π + 2πn, n ∈ Z x = π2 + πn, n ∈ Z или sinx — √32 = 0 sinx = √32 x = π3 + 2πn, n ∈ Z x = 2π3 + 2πn, n ∈ Z б)

x₁ = 5π2 x₂ = 3π — π3 = 8π3 x₃ = 7π2 Ответ: а) π2 + πn, n ∈ Z π3 + 2πn, n ∈ Z 2π3 + 2πn, n ∈ Z б) 5π2; 8π3; 7π2

Задание 14

ABCDA₁B₁C₁D₁ — прямая призма ABCD — параллелограмм M ∈ A₁B₁ K ∈ B₁C₁ N ∈ BC B₁KKC₁ = 13 AMKN — равнобедренная трапеция AN = 4, MK = 2 основания Решение: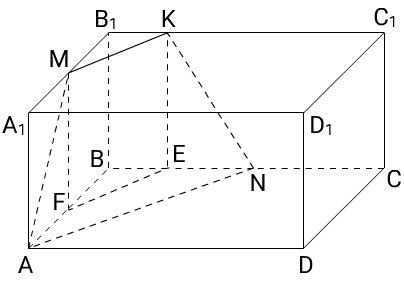

MF и KE — высоты призмы а) EF || MK, EF = MK ⇒ EF || AN, EF = 12AN Δ FBE ∼ Δ ABN, k = 12 ⇒ BN = 2BE 2BE = 2B₁K 2B₁K = 12B₁C₁ = 12BC BN = 12BC ⇒ N — середина BC б) V_призмы = 24, h = 3 ⇒ S_{основания} = 243 = 8 = S_ABCD 1) Δ AFM = Δ NEK (по катету и гипотенузе) ⇒ AF = EN 2) Δ ABN — равнобедренный с основанием AN = 4 ⇒ S_ABN = 84 = 2 ⇒ h_AN = 22 = 1 3) по теореме Пифагора найдем высоту трапеции √3² + (½)² = √9 + ¼ = √9¼ = √37/4 = √372 4) S_AMKN = 2 + 42 × √372 = 3√372 Ответ: б) 3√372

Задание 15

Решение:

2^-2√x + 32 × 10^2-√x > 2^9-2√x + 625 × 10^-2-√x 2^-2√x + 32 × 10^2-√x — 2^9-2√x — 625 × 10^-2-√x > 0 2^-2√x(1 — 2⁹) — 10^-2-√x × 625(1 — 2⁹) > 0 (1 — 2⁹)(2^-2√x — 10^-2-√x × 625) > 0 разделим обе части неравенства на (1 — 2⁹) < 0 значит знак неравенства изменится
2^-2√x — 10^-2-√x × 625 < 0 разделим обе части неравенства на 10^-√x > 0, получим 2^-√x × (210)^-√x — 1100 × 625 < 0
2^-√x × (15)^-√x — 625100 < 0
(25)^-√x < 625100 = 254 = (52)² (52)^√x < (52)² ⟺ √x < 2 x ≥ 0 x < 2² x ≥ 0 x < 4 Ответ: [0; 4)