Вариант 2, решение заданий с ответами - Ященко ОГЭ 2024 математика 36 вариантов ФИПИ

Часть 1

Задание 1

Решение: По таблице 1 выбираем размеры в порядке возрастания А6 ➔ 105 × 148 ➔ 3 А5 ➔ 148 × 210 ➔ 1 А4 ➔ 210 × 297 ➔ 4 А3 ➔ 297 × 420 ➔ 2 Ответ: 3142

Задание 2

Решение: ? листов А5 из 1 листа А2 А2 = 2А3 = 2 × 2А4 = 2 × 2 × 2А5 = 8А5 (по рисунку) Ответ: 8

Задание 3

Решение: Меньшая сторона А1? Это большая сторона А2 = 2 большим сторонам А4 = 297 × 2 = 594 мм Ответ: 594

Задание 4

Решение: S_А6 — ? см² Размеры А6 = 105 × 148 = 15540 мм² (из №1) 15540 мм² = 155.4 см² Ответ: 155.4

Задание 5

Решение: меньшая сторона А2большая сторона А2 = большая сторона А3две большие стороны А4 = 420 мм2 × 297 мм = 0.(70) ≈ 0.7 Ответ: 0.7

Задание 6

Решение: 4.23 — 23 = 4.22 33 — 23 = 4.2213 = 415 : 213 = 215 × 37 = 3 × 35 × 1 = 95 = 145 = 1.8 Ответ: 1.8

Задание 7

Решение: 4 < a < 5 по рисунку
1) 4 — a > 0 ⇒ a < 4 неверно
2) 4 — a < 0 ⇒ a > 4 верно
3) a — 3 < 0 ⇒ a < 3 неверно
4) a — 6 > 0 ⇒ a > 6 неверно Ответ: 2

Задание 8

Решение: √(-b)⁸ × b² = √b⁸ × b² = √b¹⁰ = b⁵ 2⁵ = 32 Ответ: 32

Задание 9

Решение: 5x² — 2x — 3 = 0 a = 5, b = -2, c = -3 D = b² — 4ac = (-2)² + 4 × 5 × 3 D = 4 + 60 = 64 x_1,2 = 2 ± 810 x₁ = 2 + 810 = 1010 = 1 x₂ = 2 — 810 = —610 = -0.6 Ответ: -0.6

Задание 10

Всего 40 машин Черных — 7 шт. Желтых — 19 шт. Зеленых — 14 шт. Решение: P_{зеленое такси} = 1440 = 720 P = 0.35 Ответ: 0.35

Задание 11

Решение: y = ax² + bx + c a > 0 ветви вверх
a < 0 ветви вниз
c > 0 y > 0 при x = 0
c < 0 y < 0 при x = 0
Ответ: 312

Задание 12

Решение: P = I²R P = 144.5 Вт I = 8.5 А 144.5 = 8.5² × R ⇒ R = 144.58.5² R = 144.572.25 = 2 Ответ: 2

Задание 13

Решение: 5x — 3(5x-8) < -7
5x — 15x + 24 < -7
-10x < -31
x > 3.1 (3.1; + ∞) Ответ: 4

Задание 14

Решение:

	t₀	320 мг изотоп А
8 минут	t₁	320 : 2 = 160 мг изотоп Б
8 минут	t₂	160 : 2 = 80 мг
8 минут	t₃	80 : 2 = 40 мг
8 минут	t₄	40 : 2 = 20 мг
8 минут	t₅	20 : 2 = 10 мг

5 × 8 мин = 40 мин. 160 + 80 + 40 + 20 + 10 = 310 (мг) Ответ: 310

Задание 15

Δ ABC — равносторонний треугольник BM -медиана ⇒ высота Решение:

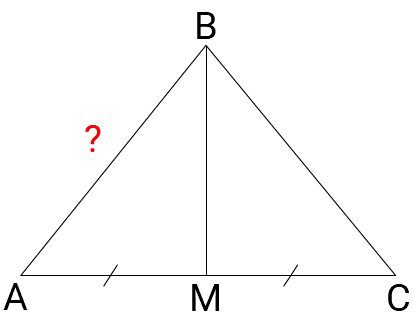
h = a√32 = BM = 12√3 a√32 = 12√3 a2 = 12 a = 24 Ответ: 24

Задание 16

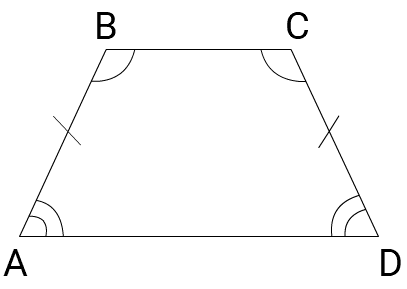
ABCD — трапеция описана около окружности. Решение:

AD и BC — основания трапеции Суммы противоположных сторон равны AD + 20 = 15 + 17 AD = 15 + 17 — 20 = 12 Ответ: 12

Задание 17

Решение:

1) ∠ B + ∠ C = 218° ∠ B = ∠ C = 218° : 2 = 109° 2) ∠ A = 180° — 109° = 71° Ответ: 71

Задание 18

Решение:

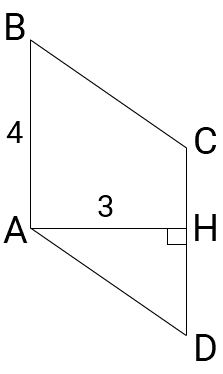
S_ABCD = CD × AH S_ABCD = 4 × 3 = 12 Ответ: 12

Задание 19

Решение: 1) ∠ A = ∠ C, ∠ B = ∠ D Верно

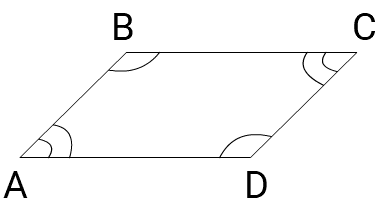
2) Δ ABC — равнобедренный с основание AC, биссектриса AD, проведенная к боковой стороне не является медианой. Неверно.

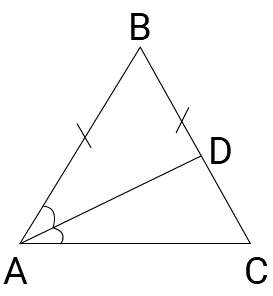
Задание 19 вариант 2 пример 2 ОГЭ математика 2024 Ященко

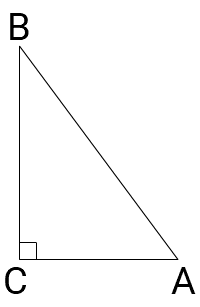
3) S_ABC = 12AC × BC Δ ABC — прямоугольный треугольник AC и BC — катеты Неверно.

Задание 19 вариант 2 пример 3 ОГЭ математика 2024 Ященко

Ответ: 1

Часть 2

Задание 20

Решение: x³ + 5x² — 4x — 20 = 0 x²(x + 5) — 4(x + 5) = 0 (x + 5)(x² — 4) = 0 (x + 5)(x — 2)(x + 2) = 0 x₁ = -5 x₂ = 2 x₃ = -2 Ответ: -5; -2; 2

Задание 21

Решение:

	V	t	S
I	x?	475x	475 км
II	x — 18	475x — 18	475 км

t₁ < t₂ на 2 часа t₂ — t₁ = 2 475x — 18 — 475x = 2 НОЗ: x(x — 18) 475x — 475(x — 18) = 2x(x — 18) 475x — 475x + 8550 = 2x² — 36x 2x² — 36x — 8550 = 0 разделим обе части равенства на 2 x² — 18x — 4275 = 0 D4 = 81 + 4275 = 4356 = 66² x_1,2 = 9 ± 66 x₁ = 9 + 66 = 75 км/ч x₂ = 9 — 66 = -57 что меньше 0 Ответ: 75

Задание 22

Решение: 1) Преобразуем функцию, раскроем знак модуля Если x ≥ 0, то y = (0.5x² + 0.5x)xx + 1 y = 0.5x²(x + 1)x + 1 = 0.5x² при x ≠ -1 Если x < 0, то y = (0.5x² + 0.5x) × (-x)x + 1 y = -0.5x²(x + 1)x + 1 = -0.5x² при x ≠ -1 2) Построим график функции

0.5x², x ≥ 0 -0.5x², x < 0, x ≠ -1

x	0	1	2
y	0	0.5	2

y(-1) = -0.5

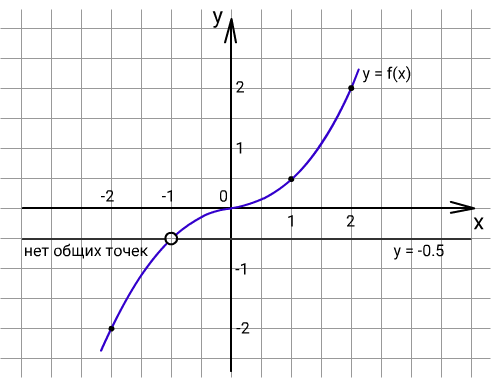
Задание 22 вариант 2 ОГЭ математика 2024 Ященко

Ответ: при m = -0.5

Задание 23

Δ ABC вписан в окружность R = 10 ∠ B = 61° ∠ C = 89° Решение: 1) ∠ A = 180° — 61° — 89° = 30° 2) По теореме синусов ВСsinA = 2R ВСsin30° = 2R ВС12 = 2R BC = R ⇒ BC = 10

Ответ: 10

Задание 24

MNPK — трапеция

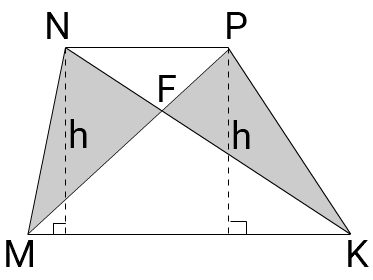
Решение: NP и MK — основания трапеции MP ∩ NK = F диагонали 1) Δ MNK и Δ MPK имеют равные высоты поэтому S_MNK = S_MPK 2) S_MNF = S_MNK — S_MFK 3) S_PKF = S_MPK — S_MFK 4) т.к. S_MNK = S_MPK (по доказанному в пункте 1) то S_MNF = S_PKF что и требовалось доказать. Ответ: S_MNF = S_PKF

Задание 25

Δ ABC, BE — биссектриса AD — медиана, BE ⊥ AD, BE = AD = 20 Решение:

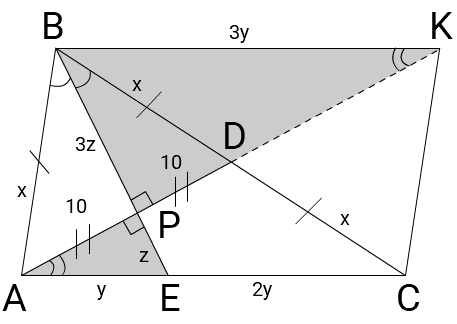
1) Рассмотрим треугольник ABD, BP — биссектриса и высота ⇒ треугольник равнобедренный с основанием AD ⇒ BD = AB и BP — медиана т.е. AP = PD = AD : 2 = 20 : 2 = 10 Пусть BD = DC = AB = x, тогда BC = 2x 2) По свойству биссектрисы в Δ ABC имеем BCBA = CEAE = 2xx = 2 т.е. CEAE = 21 ⇒ CE = 2AE Пусть AE = y, тогда CE = 2y 3) Дополнительное построение: BK || AC, BK = AC, BK = 3y 4) Δ APE ∼ Δ KPB (по двум углам) ∠ P = 90°, ∠ A = ∠ K накрест лежащие углы. Из подобия треугольников ⇒ AEBK = PEPB = y3y = 13 ⇒ PE = 14BE = 14 × 20 = 5 тогда BP = 3 × PE = 3 × 5 = 15 5) Δ ABP (∠ P = 90°) по теореме Пифагора AB = √AP² + BP² = √10² + 15² = √100 + 225 AB = √325 = 5√13 6) BC = 2AB = 2 × 5√13 = 10√13 7) Δ APE (∠ P = 90°) по теореме Пифагора AE = √AP² + PE² = √10² + 5² = √100 + 25 AE = √125 = 5√5 AC = 3AE = 3 × 5√5 AC = 15√5 Ответ: 5√13; 10√13; 15√5